Premiers pas en Machine Learning avec R. Volume 2 : la classification

Lecteurs assidus de notre blog, vous n’avez pas manqué notre premier billet sur le machine learning, traitant de la régression linéaire. Mais voilà, depuis ce jour, une question vous hante : à quand le deuxième volet de cette série ? Rassurez-vous : l’attente est désormais terminée.

Encore du machine learning ?

Vous le savez, le sujet est en vogue : nous vous le répétons d’ailleurs assez souvent. C’est pourquoi nous n’allons pas une nouvelle fois introduire par la définition du machine learning, et vous répéter que « l’apprentissage automatique regroupe l’ensemble des techniques qui permettent d’évaluer des données nouvelles et de réaliser une prédiction basée sur les connaissances tirées de données anciennes ». Eh non, nous allons directement entrer dans le vif du sujet !

Machine learning 102 : la classification

« Bon, de quoi est-il question aujourd’hui ? » Tout est dans le nom ! Cette famille d’algorithmes de machine learning se destine à classer l’information nouvelle dans l’une des catégories des données anciennes — ce tri s’appuyant sur une estimation probabiliste de l’appartenance à une classe. L’exemple le plus populaire reste celui du traitement des spams : en se basant sur un corpus d’emails, l’algorithme étiquète un nouveau message en « spam » ou « non-spam ».

Passons à une représentation de ce modèle de classement, pour les plus visuels d’entre vous. Imaginons une série d’individus en entrée, tous accompagnés :
– De variables : « ont des poils (oui / non) », « ont une moustache (oui / non) », « aiment la pâté (oui / non) », « jouent avec une balle (oui / non) ».
– Une classe en sortie : si ces individus sont des hommes, ou des chats.

Nous pouvons ainsi décrire chaque observation selon une suite de ces modalités : oui / oui / oui / oui, oui / non / non / oui, et ainsi de suite. Chaque classe de sortie (homme / chat) se retrouvant étiquetée d’une ou plusieurs de ces suites. Il est alors possible de visualiser ces données sous forme d’un arbre de décision, chaque niveau de cet arbre correspondant à une variable, et chaque branche une suite de modalités des variables.

Et sur votre gauche, une représentation de cet arbre !

Ensuite, comment faire une prédiction ? Chaque nouvel individu est « lâché » à la pointe de l’arbre, et suit un chemin en fonction de ses modalités de variables, avant d’arriver à une estimation de classe. Par exemple, un entrant avec des variables 1 à tous les niveaux (un individu qui a des poils, une moustache, aime la pâté et jouer avec une balle) sera assigné à la classe chat avec une certaine probabilité — même si un humain peut-être moustachu, jouer avec une balle et manger de la pâté, cela reste minoritaire, et sûrement peu représenté dans le jeu de données d’apprentissage. À l’inverse, un chat siamois n’aura pas de poils, mais présentera toutes les autres caractéristiques (0/1/1/1).

Votre premier algorithme de classification avec R

Alors, comment ça marche avec R ? Pour votre premier algo de classification, nous allons prendre un dataset bien connu : celui des survivants du Titanic. Plusieurs jeux de données circulent sur le web, nous avons choisi celui disponible sur la page du département de biostatistiques de l’université Vanderbilt.

Ce dataset contient, comme son nom le laisse entendre, la liste des passagers du Titanic, s’ils ont ou non survécu au naufrage, ainsi que plusieurs variables descriptives : leur âge, la classe d’embarquement, le sexe, etc.

# Chargement des packages du tidyverse, et du jeu de données
> library(tidyverse)
> titanic <- read_csv("http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic3.csv")

Avant d’entrainer notre modèle, il est nécessaire de le « découper », afin de pouvoir en mesurer l’efficacité. Les proportions idéales ? Bonne question, chacun y va de son pronostic. Et au fond, il peut être intéressant de tester plusieurs découpages lors de l’analyse. Mais un point de départ solide reste 80/20 — c’est celui que nous allons utiliser ici.

> #Séparation jeu de données
> set.seed(2811)
> train <- titanic %>% sample_frac(0.8)
> test <- anti_join(titanic, train)

Maintenant, comment créer un modèle de classification ? Pour cela, direction le package rpart. La formule à utiliser devrait vous rappeler celle du modèle linéaire :  model <- rpart(variableàexpliquer ~ variableexplicative, data = jeudedonnées, method = "class"). Nous ajoutons l’élément method = "class" pour signifier que la variable à expliquer est un facteur. Ensuite, que fait-on avec notre modèle ? On le teste sur… le jeu de données test, tout simplement ! Pour cela, on se rappelle la fonction predict de notre premier billet — la voici de retour, avec l’argument type = "class".

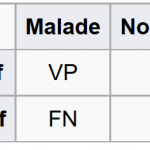
Cependant, ce n'est pas tout ! Il est important de pouvoir estimer la qualité de notre modèle. Pour cela, plusieurs indicateurs sont utilisables, comme par exemple le taux de bons classements. Un ratio simple à obtenir, mais parfois peu informatif, notamment pour les événements rares. Alors, que faire vous dites-vous ? Utiliser ce que l'on appelle une matrice de confusion, croisant les vrais / faux positifs, et les vrais / faux négatifs.

Dans ce tableau, affichant les résultats d'un test médical, VP (vrais positifs) représente le nombre d'individus malades avec un test positif, FP (faux positifs, ou erreur de type 1) le nombre d'individus non malades avec un test positif, FN (faux négatifs, ou erreur de type 2) le nombre d'individus malades avec un test négatif, et VN (vrais négatifs) représente le nombre d'individus non malades avec un test négatif.

Cette table vous permet de calculer deux indicateurs, que l'on appelle sensibilité et spécificité — respectivement, dans notre exemple, la probabilité que le test soit positif si la maladie est présente (et qui se calcule VP / VP + FN), et la probabilité d’obtenir un test négatif chez les non-malades (VN / VN + FP). Autrement dit, la sensibilité est la capacité d'un modèle à prédire un positif quand la donnée est réellement positive, et la spécificité, sa capacité inverse, celle de prédire un négatif lorsqu'il y a vraiment un négatif. Pourquoi utiliser ces deux indices en complément ? Parce qu'un bon modèle doit être à la fois sensible et spécifique — en effet, un modèle qui vous prédira un positif dans 100 % des cas sera très sensible, mais sa spécificité sera mauvaise.

"Faut faire tout ça à la main ?" Pas forcément, lecteur, et vous pouvez appeler le package caret est à la rescousse — ce dernier produit une matrice de confusion avec la fonction confusionMatrix(variablespredites, variabledereference), et la sensibilité et la spécificité sont ensuite calculées automatiquement.

Il existe d'autres méthodes de calcul de performance, comme par exemple l'utilisation d'un courbe ROC, ou encore l'indice de Youden. Mais nous n'allons pas vous noyer sous les concepts (ça sera pour une prochaine fois), car il est temps de...

... Mettre la main à la pâte !

Commençons d’abord par une prédiction univariée : obtient-on de meilleurs résultats en utilisant la variable sexe, class ou age?

> library(rpart)
> library(caret)
> tree <- rpart(survived ~ sex, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
  0.8554217 
> conf$byClass["Specificity"]
Specificity 
  0.6979167 
> 
> tree <- rpart(survived ~ pclass, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
  0.8012048 
> conf$byClass["Specificity"]
Specificity 
  0.3854167 
> 
> tree <- rpart(survived ~ age, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
  0.9638554 
> conf$byClass["Specificity"]
Specificity 
    0.09375 

Qu'en déduire ? Les différents modèles, basés sur plusieurs variables, affichent des performances différentes : les variable age et pclass permettent une haute sensibilité, mais réussissent moins bien du côté de la spécificité. Il semblerait que la variable la plus performante (pour de l'univarié) soit sex.

Ensuite, comment affiner le modèle ? En passant à une prédiction multivariée. Et l’ajout d’une nouvelle variable est assez simple : il suffit de la combiner avec +, à la suite de la première variable explicative.

> #Prédiction multivariée
> 
> tree <- rpart(survived ~ sex + pclass, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
  0.8554217 
> conf$byClass["Specificity"]
Specificity 
  0.6979167 
> 
> tree <- rpart(survived ~ sex + pclass + parch, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
  0.8975904 
> conf$byClass["Specificity"]
Specificity 
    0.65625 
> 
> tree <- rpart(survived ~ sex + pclass + parch + embarked, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
   0.939759 
> conf$byClass["Specificity"]
Specificity 
  0.6145833 
> 
> tree <- rpart(survived ~ sex + pclass + parch + embarked + sibsp, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
   0.939759 
> conf$byClass["Specificity"]
Specificity 
  0.6145833 
> 
> tree <- rpart(survived ~ sex + pclass + parch + embarked + sibsp + fare, data = train, method = "class") 
> test$prediction <- predict(tree, test, type = "class")
> conf <- confusionMatrix(data = test$prediction, reference = test$survived)
> conf$byClass["Sensitivity"]
Sensitivity 
  0.8915663 
> conf$byClass["Specificity"]
Specificity 
  0.6979167 

Ces modèles nous affichent des performances relativement semblables : la sensibilité oscillant entre 0.85 et 0.94, et la spécificité entre 0.61 et 0.69. La prochaine étape pour un modèle encore meilleur ? Des sous-ensembles différents, entrainants plusieurs modèles. Une technique appelée Random Forest, ou Forêt d’arbres décisionnels dans la langue de Molière. Mais ça, ce n’est plus à un niveau introductif, et nous en parlerons une prochaine fois !