Premiers pas en Machine Learning avec R. Volume 4 : random forest

Quatrième volet de notre série sur le machine learning, avec au programme du jour les Random Forests, ou Forêts aléatoires / Forêts d’arbres décisionnels, pour les plus accrochés à la langue de Molière.

Random whaaaaat ?

Bon, revenons aux bases : qu’est qu’un « arbre décisionnel » ? Si vous avez séché notre second volet sur le machine learning, il est toujours temps de réviser 😉

Pour vous donner la version courte, un arbre de décision est une visualisation graphique sous forme d’arbre (comme son nom l’indique), d’une suite de décisions / possibilités. Chaque point est un noeud, et chaque lien entre les noeuds s’appelle branche.

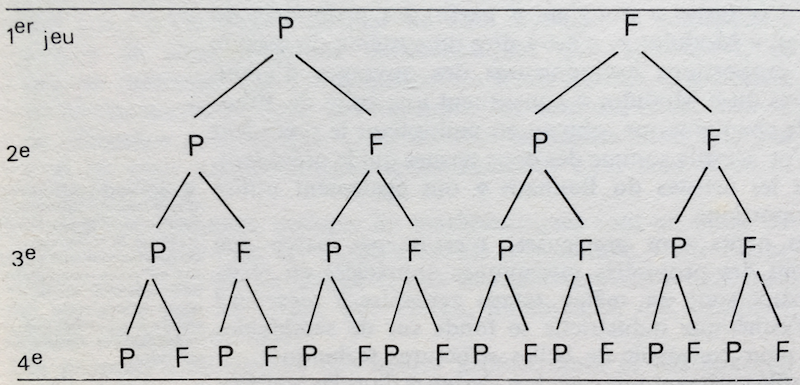
Par exemple, voici la représentation de toutes les variations d’une série de 4 tirages à pile ou face.

Le point de départ se situe au sommet de l’arbre (appelé root), et la décision / l’état final se trouve à l’autre extrémité : cet état étant atteint en suivant un chemin défini par les étapes intermédiaires, qui sont à chaque noeud séparé en deux sous-groupes. Par exemple, ici, la situation de départ « obtenir quatre piles » est obtenue si à chaque tirage, l’arbre construit une branche vers pile.

Bien, en quoi ça nous aide à faire du machine learning tout ça ? Et bien parce qu’on peut donner une probabilité à chaque décision. Pour poursuivre notre exemple de pile ou face, chaque noeud a une probabilité de 0.5 de retomber sur pile : en connaissant, cette probabilité, il est possible de calculer une probabilité pour chaque résultat, chaque « chemin » suivi par l’arbre.

• Pour 4 piles, soit P/P/P/P : 0.5 * 0.5 * 0.5 * 0.5 = 0.0625, soit 1 chance sur 16.
• Pour 3 piles, les choses se complexifient, puisqu’il existe 4 chemins distincts : P/P/P/F, P/P/F/P, P/F/P/P et F/P/P/P. Nous avons : (0.5 * 0.5 * 0.5 * 0.5) * 4 = 0.25, soit une chance sur 4.

Et ainsi de suite.

« Et le machine learning dans tout ça ? » On y vient, on y vient. Donc, imaginons une série d’observations étiquetées A et B, avec des variables a, b, c et d, chacune à deux modalités 1/2 (oui, ça ressemble à notre situation du dessus). Nous souhaitons effectuer une prédiction sur des données nouvelles, afin de leur assigner une appartenance à A ou B, en connaissant uniquement les modalités des variables. Notre modèle de machine learning va construire un arbre de décision basé sur les données existantes, en affectant une probabilité à chaque combinaison chemin/point de sortie. Par exemple, et au hasard, si la probabilité de suivre 1/1/1/1 est de 80% pour le label A, chaque observation qui suit ce chemin se verra assigner ce label.

Digression : arbres de régression et arbres de classification

digression::on()

Si vous avez bien suivi, vous avez compris que l’on part du haut de l’arbre, pour « spliter », c’est-à-dire segmenter en sous-groupe à chaque niveau, en fonction d’un critère. Par exemple, pour notre pile ou face, les noeuds sont splités selon le critère P/F à chaque noeud. Cet exemple est très simpliste : dans la pratique, ce n’est pas à vous de définir le paramètre de découpage de chaque noeud. Cette sélection est effectuée par l’algorithme, qui s’adapte au type d’arbre : de régression ou de classification.

Arbre de régression

On parle d’arbre de régression quand la variable dépendante (celle que nous cherchons à prédire) est continue. À chaque niveau, la séparation s’effectue afin de composer deux groupes avec la variance inter-classe maximale, généralement avec un test du khi deux.

L’arbre de régression présente le désavantage de ne pas pouvoir extrapoler hors du jeu de données de départ. Autrement dit, là où une régression linéaire est continue, et est donc applicable à des valeurs nouvelles à l’infini, l’arbre de régression ne permet « que » de prédire un chiffre appartenant au jeu de départ. En clair, un modèle de régression linéaire Y = ax + b est déclinable à tout x, à l’inverse d’un arbre de régression.

Arbre de classification

L’arbre de classification, quant à lui, est la déclinaison de l’arbre pour les situations où la variable dépendante est catégorielle. Le critère le plus connu de segmentation étant l’indice d’impureté de Gini, notamment utilisée par l’algorithme CART.

Le concept de pureté fait référence au caractère discriminant de la séparation effectuée par un noeud. En clair, une séparation est dite pure quand chaque partie post-split contient des éléments d’une même classe. À l’inverse, le maximum d’impureté est atteint lorsque chaque séparation contient la même probabilité d’éléments de chaque classe. Imaginons un dataset contenant AABB — la segmentation la plus pure classe en deux groupes AA et BB, et la plus impure en AB et AB. Dans le cas du random forest, il s’agit donc de trouver la segmentation qui donne des résultats le plus purs possibles.

C’est sur la classification que les Random Forests sont les plus intéressantes.

L’algorithme CART

Acronyme de Classification And Regression Trees, cet algorithme produit un modèle croisant arbre de régression et arbre de classification : autrement dit, il s’agit d’un modèle qui s’adapte à (presque) tous les jeux de données.

digression::off()

La forêt d’arbres aléatoires

Bon, retour à nos moutons : les forêts d’arbres aléatoires. Si vous vous êtes bien accroché jusqu’ici, vous avez déjà deviné le fonctionnement de cette méthode de machine learning : avec une Random Forest vous construisez une « forêt d’arbres » (donc, plusieurs arbres de décision), de manière aléatoire (eh oui, tout est dans le nom). C’est pour cela que l’on parle de « ensemble method » pour qualifier cette approche : une multitude de modèles « faibles » sont combinés pour créer un modèle robuste.

Une fois ce modèle construit, les données nouvelles sont « lancées » dans tous les arbres, qui votent pour la classe de sortie : pour une régression, en faisant une moyenne, pour une classification en votant à la majorité.

Pourquoi choisir une Random Forest ?

Bonne question, lecteur ! Eh bien, un modèle de forêt aléatoire est un bon choix pour les raisons suivantes :

• Il est plus simple à mettre en place, en ce sens qu’une Random Forest combine régression et classification, ce qui permet de gagner du temps sur la préparation des données.
• Il y a moins de chance « d’overfitting » (ces cas où le modèle est parfaitement adapté aux données, mais se généralise très mal)
• Une précision plus fine des prédictions : la Random Forest n’effectue pas de pruning.

digression::on()

Le pruning est une méthode utilisée pour prévenir l’overfitting des arbres de décision, en taillant certains niveaux de l’arbre.

digression::off()

Vous vous posez la question : qu’est-ce qui est aléatoire dans un arbre aléatoire ? Bien vu ! Cette méthode de machine learning compte deux grands pans d’aléatoire : (1) dans le sampling sur lesquels sont construits les arbres (2) dans la sélection des variables sur lesquelles sont effectuées la segmentation.

Et en gros, comment ça se passe ?

La forêt aléatoire reste une boîte noire dans de nombreux cas : et pour cause, si vous construisez une forêt de 500, 1000, voire 10.000 (soyons fous) unités, vous ne pourrez pas avoir un regard sur le mécanisme de chaque arbre. Mais, voici globalement comment cela se passe, si nous voulons 500 arbres :

• 500 subsets de nos données sont pris aléatoirement, avec remplacement. En général, ces samples font chacune 2/3 de l’ensemble.
• Pour chaque sous-groupe, un arbre de décision est créé.
• Des variables de segmentation sont choisies aléatoirement, et l’arbre est splité en suivant la meilleure segmentation.
• Chaque arbre est poussé à son maximum, sans « pruning ».
• Nous voici avec 500 modèles différents, avec des calculs de précisions sur le 1/3 de données non utilisés (nous en reparlerons plus bas.)
• Lorsque des données nouvelles sont présentées au modèle, elles seront évaluées par tous les arbres.

Une Random forest avec R

Bon, passons maintenant aux choses sérieuses : mettre en place une Random Forest avec R.

# install.packages("randomForest") 
library(randomForest)

Obtenir des données (et les nettoyer)

Sans données, pas de machine learning ! Pour entraîner notre modèle, nous allons piocher dans un jeu de données disponible sur le site d’open data de l’éducation nationale : Effectifs des personnels des écoles du 1er degré et des établissements du 2nd degré. Le dataset étant national, nous avons réduit la voilure : le jeu de données complet compte, après transformation, 910059 individus… ce qui demande un peu de temps de traitement par votre ordinateur, nous avons donc réduit à l’académie de Rennes, pour l’exemple.

library(tidyverse)
educ <- read.csv2("https://data.education.gouv.fr/explore/dataset/fr-en-effectifs-des-personnels-des-ecoles-et-etablissements-du-2nd-degre/download/?format=csv&timezone=Europe/Berlin&use_labels_for_header=true")
set.seed(2811)

Le nombre d'agents est compté dans la colonne Nombre.d.agents. Seulement voilà, avec une colonne contenant le nombre d'agents, notre tableau n'est pas vraiment tidy : une ligne ne correspond pas à un individu. Lançons-nous d'abord dans un peu de data wrangling :

educ_small <- educ %>%
  filter(Académie == "RENNES") %>%
  select(Type.d.établissement, Secteur.d.enseignement,
         Groupe.de.personnels, Titulaire, Sexe, Borne.inférieure.de.la.tranche.d.âge, Nombre.d.agents, 
         Code.région)

sum(educ_small$Nombre.d.agents)
[1] 43510
nrow(educ_small)
[1] 16248

educ_small <- educ_small %>% 
  mutate(Idx = 1:n()) %>% 
  group_by(Idx) %>%
  mutate( Agent = list(rep( Sexe, Nombre.d.agents) ) ) %>%
  unnest() %>%
  ungroup()
  select(-Idx)

nrow(educ_small)
[1] 43510

Et voilà !

Train and test

Same old same old : on crée son modèle sur une partie de ses données, et on effectue les prédictions sur une partie test. Ici, nous allons essayer de prédire la variable binaire Titulaire.

Note : en théorie, nous n'aurions pas besoin de fractionner nos dataset en train et test (nous vous l'expliquons juste après). Cependant, on est jamais trop prudent, et effectuer une double validation sur un jeu de données test est (1) une bonne pratique, (2) un filet de sécurité.

train <- educ_small %>% sample_frac(0.8)
test <- anti_join(educ_small, train)
library(randomForest)
(model <- randomForest(Titulaire ~ ., data = train, ntree = 500, na.action = na.omit))
# Peut prendre un peu de temps :)

Call:
 randomForest(formula = Titulaire ~ ., data = train, ntree = 500,      na.action = na.omit) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 3

        OOB estimate of  error rate: 3.97%
Confusion matrix:
            Contractuel Titulaire class.error
Contractuel       14725       820  0.05275008
Titulaire           551     18439  0.02901527

Prenons un instant pour expliquer l'output de notre modèle.

• Sans surprise, vous trouvez le Call, qui est notre fonction d'appel : le classique variable_dependante ~ ., le data, et des petits nouveaux : ntree (vous vous en doutez, le nombre d'arbres à créer), et na.action, qui est l'action à effectuer face aux NA. Car oui, la Random Forest ne gère pas les données manquantes à votre place, et vous renverra une erreur s'il en trouve. Vous pouvez spécifier : na.omit, qui retirera les données manquantes, ou encore na.roughfix, qui les remplace par des valeurs médianes.

• Le type d'arbre (ici, de classification) et le nombre d'arbres

• Le nombre de variables testées lors du split de chaque noeud

• Le "Out Of Bag estimate of error rate"

• La matrice de confusion

Revenons sur ces deux derniers :

Out Of Bag estimate of error rate

Comme vous le savez, chaque arbre est entraîné sur une fraction des data, qui est considérée comme "in-bag". Ce qui permet à chaque arbre, une fois construit, d'estimer son taux d'erreur sur les données qu'il a laissé "out-of-bag" : plus ce taux est faible, plus le modèle est juste. Ce chiffre à lui seul pourrait servir d'indicateur de performance du modèle.

Vous pouvez accéder au nombre de fois qu'un individu a été laissé "out of bag" en avec model$oob.times. Si nous dressons un histogramme :

hist(model$oob.times)

Confusion matrix

Pour un rappel sur les confusions matrix, direction notre billet précédent Premiers pas en Machine Learning avec R. Volume 2 : la classification, section "Votre premier algorithme de classification avec R" !

Rapidement : en colonne, la prédiction de l'algo, et en ligne la modalité réelle. En clair, dans notre modèle, 14725 individus de la classe réelle "Contractuel" ont été affectés à la bonne classe. La diagonale représente le nombre de bien classés pour toutes les modalités. Juste à côté, le class.error indique la proportion de mauvais résultats.

Autres informations du modèle

L'élément votes de votre modèle vous renvoie la répartition des votes pour chaque individu.

model$votes[1:10,]
   Contractuel   Titulaire
1  0.984042553 0.015957447
2  0.004854369 0.995145631
3  1.000000000 0.000000000
4  0.021978022 0.978021978
5  0.994382022 0.005617978
6  0.000000000 1.000000000
7  0.327956989 0.672043011
8  0.005405405 0.994594595
9  0.000000000 1.000000000
10 1.000000000 0.000000000

Ici, on voit que le premier individu a été classé en Contractuel dans 98,4% des cas où il était "OOB", et 1,6% des fois en Titulaires.

L'importance des variables

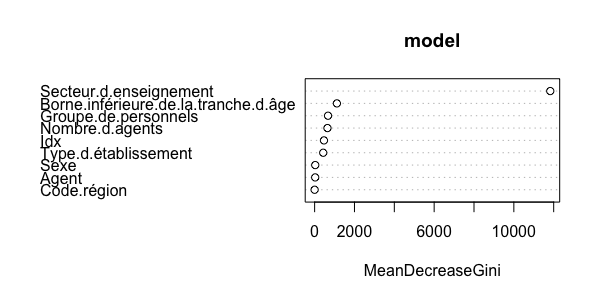
Le modèle de Random Forest renvoie également un objet importance : il s'agit là de la diminution moyenne de l'impureté apportée par chaque variable. Elle est calculée par l'index de Gini : la diminution pour chaque noeud est cumulée, puis une moyenne sur l'ensemble des arbres est effectuée. Cet indicateur se trouve ensuite dans votre modèle :

model$importance
                                     MeanDecreaseGini
Type.d.établissement                        431.17664
Secteur.d.enseignement                    11827.79572
Groupe.de.personnels                        672.62899
Sexe                                         30.91989
Borne.inférieure.de.la.tranche.d.âge       1118.20841
Nombre.d.agents                             644.13835
Code.région                                   0.00000
Idx                                         468.89870
Agent                                        28.45086

# Vous pouvez le visualiser avec randomForest::varImpPlot()

varImpPlot(model)

Predict

Bien, au tour d'une prédiction maintenant !

test$predicted <- predict(model, test)

Réalisons une matrice de confusion. Pour rappel, la sensibilité est la capacité du modèle à prédire un vrai positif et la spécificité la capacité à prédire les vrais négatifs. Ici, si nous prenons la classe Contractuel comme classe de référence, la sensibilité mesure la capacité du modèle à prédire Contractuel lorsque la classe réelle est Contractuel, et la spécificité la capacité de prédire Titulaire lorsque la classe est Titulaire.

Vous obtenez cette matrice avec :

table(test$predicted, test$Titulaire) 
              Contractuel Titulaire
  Contractuel         731        79
  Titulaire            90      1026

Mais rappelez-vous, la library caret peut le faire pour vous !

library(caret)
conf <- confusionMatrix(data = test$predicted, reference = test$Titulaire)

conf$byClass["Sensitivity"]
Sensitivity 
  0.8903776 
  
conf$byClass["Specificity"]
Specificity 
  0.9285068 

Résultat ? Notre modèle prédit de manière juste Contractuel dans 89% des cas, et Titulaire dans 93%. Pas mal non ?

Paramétrer son modèle

Bien, c'est beau tout ça, mais nous n'avons pas trop la main sur ce qu'on envoie dans notre algorithme ! Tu as raison lecteur, c'est pourquoi voici quelques idées pour aller plus loin.

Augmenter le nombre d'arbres

Un modèle de forêts aléatoires a une part... d'aléatoire, qui est un potentiel de biais d'échantillonnage. Tout ça peut être compensé par une augmentation du volume d'arbres. Attention, plus le nombre d'arbres évolue, plus le temps de calcul est long. Comparons trois paramétrages :

(model50 <- randomForest(Titulaire ~ ., data = train, ntree = 50, na.action = na.omit))

        OOB estimate of  error rate: 3.94%
Confusion matrix:
            Contractuel Titulaire class.error
Contractuel       14787       758  0.04876166
Titulaire           602     18388  0.03170090

(model500 <- randomForest(Titulaire ~ ., data = train, ntree = 500, na.action = na.omit))

        OOB estimate of  error rate: 3.87%
Confusion matrix:
            Contractuel Titulaire class.error
Contractuel       14775       770  0.04953361
Titulaire           566     18424  0.02980516

(model1000 <- randomForest(Titulaire ~ ., data = train, ntree = 1000, na.action = na.omit))

        OOB estimate of  error rate: 3.84%
Confusion matrix:
            Contractuel Titulaire class.error
Contractuel       14783       762  0.04901898
Titulaire           564     18426  0.02969984

On voit qu'augmenter drastiquement le nombre d'arbres n'améliore pas significativement le taux d'erreur, mais multipliera le temps de calcul.

Quelques paramètres en plus

Des paramètres ont été pensés pour jouer sur le temps de calcul et/ou sur la précision :

• mtry : le nombre de variables testées à chaque split. La valeur par défaut étant la racine carrée du nombre de variables. C'est le principal paramètre à modifier, avec ntree.

• subset : pour ne travailler que sur certaines parties de votre jeu de données.

• replace : le sampling est-il fait avec ou sans remplacement ?

• nodesize : la taille maximale des noeuds (plus elle est élevée, plus les arbres seront courts).

• importance : le modèle doit-il évaluer l'importance des variables ?

Par exemple, si l'on passe tout cela dans un microbenchmark (le temps d'aller faire couler un café).

# Testons sur un petit jeu de données : iris
# En augmentant le nombre d'essais à chaque split

library(microbenchmark)
mb <- microbenchmark(times = 100, 
                      un = randomForest(Species ~ ., data = iris, ntree = 500, na.action = na.omit, mtry = 1), 
               deux = randomForest(Species ~ ., data = iris, ntree = 500, na.action = na.omit, mtry = 2), 
               trois = randomForest(Species ~ ., data = iris, ntree = 500, na.action = na.omit, mtry = 3), 
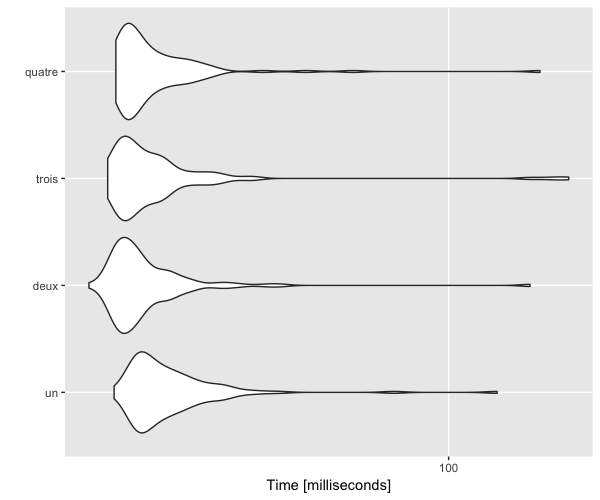
               quatre = randomForest(Species ~ ., data = iris, ntree = 500, na.action = na.omit, mtry = 4))
autoplot(mb)

mb_2 <- microbenchmark(times = 100, 
                      avec = randomForest(Species ~ ., data = iris, ntree = 500, na.action = na.omit, importance = TRUE), 
               sans = randomForest(Species ~ ., data = iris, ntree = 500, na.action = na.omit, importance = FALSE))

autoplot(mb_2)

Avec CARET

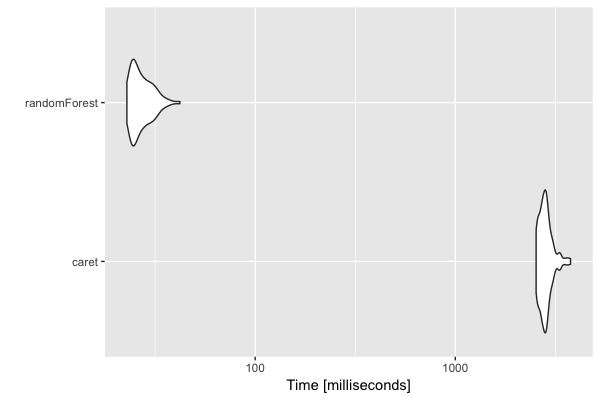
La librairie caret, pour Classification And REgression Training, offre aux utilisateurs une grande variété d'algorithmes de machine learning, hautement personnalisable. Le prix ? Un temps de traitement un peu plus long si on ne paramètre pas correctement l'algorithme.

Par exemple, si on cherche à construire un seul arbre, sans plus de paramètres (hormis na.action).

mb_3 <- microbenchmark(times = 100, 
                      caret = train(Species ~ ., data = iris,na.action = na.omit),
                      randomForest = randomForest(Species ~ ., data = iris, na.action = na.omit))

autoplot(mb_3)

Vous l'avez compris, pour faire une Random Forest avec ce package, direction la fonction train(), qui recevra method = "rf" en paramètre. Ensuite, nous vous conseillons de bien régler votre fonction, si vous ne souhaitez pas vous retrouver à mettre 8 heures à faire tourner votre code… D'autres algorithmes de Random Forest sont disponibles, vous pouvez les consulter ici.

Bien sûr, vous pouvez également triturer votre modèle : nombre d'arbres, nombre d'essais pour les splits, et bien d'autres. D'autres librairies existent, mais nous ne pouvons pas vous faire un tour d'horizon de toutes celles-ci ici... cela dit, on peut en reparler !