Parce que couvrir un sujet aussi large que le text-mining ne pouvait pas se faire en un billet de blog, voici le troisième volet de notre série sur le text-mining avec R.
Sommaire
Topic modeling
Nous avons déjà vu sur ce blog deux approches : comment faire vos premiers pas avec une méthode basique d’analyse fréquentiste, en comparant {tidytext} et {tm} dans notre premier billet. Nous avons poursuivi avec les n-grammes dans notre second numéro. Suite des hostilités aujourd’hui avec le topic modeling.
Avant toute chose, la grande question : qu’est-ce que le topic modeling ? En NLP (Natural Language Processing), un topic model fait référence à un modèle probabiliste, définissant l’appartenance de documents à des topics, ou thèmes. À première vue, ce modèle est assez intuitif, vous allez très vite comprendre pourquoi. Lorsque vous lisez un texte, vous vous attendez à ce que ce document contienne de nombreux n-grammes en rapport avec un sujet spécifique. Car oui, vous partez du postulat qu’un auteur commence à écrire en ayant une ou plusieurs thématique(s) à l’esprit, et qu’il utilise ensuite les mots de sa langue pour parler de cette/ces thématique(s). Par exemple, des livres sur R ont une forte probabilité de contenir des termes en rapport avec le code et la data science, comme « statistiques », « package », « fonctions », etc., à l’inverse d’un roman de Proust. C’est exactement cette idée qui sous-tend le topic modeling : un corpus est une collection de documents, un document est une collection de thématiques, et une thématique est une collection de mots.
Cette approche s’utilise plus particulièrement lors de l’analyse de corpus, afin de découvrir les spécificités propres à chaque document de la collection, afin de les regrouper par similarité. L’objectif étant de pouvoir trier, comprendre, indexer et résumer de larges séries de documents.
Le topic modeling, dans son ensemble, se découpe en trois étapes :
+ Découvrir les topics contenus dans une collection.
+ Annoter les documents en fonction de ces topics.
+ Utiliser ces annotations pour organiser et de répertorier les documents.
Par exemple, le topic modeling est utilisé par les moteurs de recherche, afin d’indexer et classer les pages qu’il rencontre, dans le but ultime de répondre de la manière la plus juste lorsque vous effectuez une requête.
Un peu de théorie
Il existe de nombreux algorithmes pour créer ces modèles, et nous allons aujourd’hui nous concentrer sur le plus utilisé d’entre eux : l’Allocation de Dirichlet latente.
Derrière ce nom un peu barbare se cache un modèle probabiliste expliquant des observations à l’aide de groupes (non observés) de données similaires. Il s’agit d’un algorithme d’apprentissage automatique non supervisé, les classes de sortie n’étant pas étiquetées. En clair, l’algorithme n’est pas à même de vous dire « ah dis donc, je pense que ces articles parlent de finance, et ceux-là de planche à voile ». Il sera « seulement » en mesure de vous dire « ces documents me semblent faire partie d’un même thème 1, dont voici les termes principaux, et celui d’un même thème 2, dont voici les termes principaux » . Oui, comme le k-mean clustering, tout à fait.
Comment ça marche ? On commence par définir un nombre k de thèmes. Ensuite, l’algorithme ira partitionner les documents, et vous répondra de deux manières :
+ en attribuant à chaque mot une probabilité d’avoir été généré par chaque thème.
+ en attribuant à chaque document une probabilité d’appartenance à chaque thème.
Et ce qu’il se passe, sous le capot :
+ LDA assigne aléatoirement à chaque mot un topic (admettons A ou B).
+ LDA parcourt chaque document mot à mot, et met à jour les topics de chaque entrée, par un calcul de probabilité dont nous vous épargnons le détail ici (mais si vous êtes un peu maso / curieux : Latent Dirichlet Allocation).
+ Ce processus d’assignation est répété de nombreuses fois jusqu’à stabilité du modèle (et… oui, comme le k-mean clustering, tout à fait).
But… why?
Pourquoi choisir cet algorithme ? La force du LDA est qu’il considère qu’un document est une composition de topics, et que ces topics peuvent être distribués sur plusieurs documents : un document A peut-être composé de 30 % de topic 1 et de 70 % de topic 2, et un document B peut-être composé de 80 % de topic 1 et de 20% de topic 2. Et non, pas comme le k-mean, cette fois : le LDA autorise un « overlap » des topics d’un document à l’autre, pour une catégorisation plus souple, et donc plus précise.
Dans R, une fois votre algorithme tourné, vous obtiendrez une liste de résultats, avec deux matrices à regarder :
beta, qui contient les probabilités de chaque mot d’avoir été généré par un topic.gamma, avec la probabilité de chaque document d’appartenir à un topic.
Encore un peu vague ? Mettons les mains dans le code, cela sera plus clair !
En pratique
Pour réaliser le topic modeling, nous aurons besoin du package {topicmodels}. Et pour l’exemple, commençons par un corpus de documents simple : quatre pages Wikipédia avec quatre topics très différents.
Ici, intuitivement, nous trouvons 4 topics. Toujours pour l’exemple, nous allons voir comment, même si nous n’avions pas l’intuition de ces topics, l’algorithme est en mesure de nous livrer un modèle qui classera chaque page dans un topic différent.
# Si besoin
install.packages("topicmodels")
install.packages("tidytext")
install.packages("tidyverse")
install.packages("rvest")
# Charger les packages
library(tidytext)
library(topicmodels)
library(tidyverse)
library(rvest)
# Créer le tibble avec les textes
## Une fonction pour scraper et créer un df
scrape_wiki <- function(url){
url <- read_html(url)
df <- tibble(text = url %>% html_nodes("p") %>% html_text(),
name = url %>% html_nodes("h1") %>% html_text())
return(df)
}
url_list <- c("https://en.wikipedia.org/wiki/Marcel_Proust",
"https://en.wikipedia.org/wiki/Natural_logarithm",
"https://en.wikipedia.org/wiki/Kreator",
"https://en.wikipedia.org/wiki/Open-source_model")
data <- map_df(.x = url_list, .f = scrape_wiki)
Nous voici donc avec un corpus de 4 documents. Le package {topicmodel} travaillant avec des DocumentTermMatrix, nous devons faire appel à la fonction cast_dtm, de {tidytext}. (Si vous avez besoin de vous rafraîchir la mémoire sur tidytext, nous vous conseillons de relire les deux billets que nous avons cités dans l'introduction ;))
# Générons le tibble avec le compte des mots, avant de le transformer en DTM
dtm <- data %>%
unnest_tokens(word, text) %>%
count(name, word, sort = TRUE) %>%
anti_join(tidytext::stop_words) %>%
#Tranformer en DocumentTermMatrix
cast_dtm(name, term = word, value = n)
class(dtm)
[1] "DocumentTermMatrix" "simple_triplet_matrix"
# Créer le modèle
lda_model <- LDA(x = dtm, k = 4, control = list(seed = 2811))
Une fois ce modèle en place, nous pouvons le faire "revenir dans le tidyverse" grâce à la fonction tidy, exportée du package {broom}.
# Avec la matrice beta
tidy_model_beta <- tidy(lda_model, matrix = "beta")
# Quelle est la probabilité que le terme logarithm soit généré par
# un des quatre topics ?
tidy_model_beta %>%
filter(term == "logarithm")
# A tibble: 4 x 3
topic term beta
1 1 logarithm 3.803857e-32
2 2 logarithm 1.261209e-37
3 3 logarithm 3.377426e-35
4 4 logarithm 5.313589e-02
Ici, nous avons un data.frame contenant les probabilités que le mot "logarithm" ait été généré par chaque topic : 5% pour le topic 4, et... très peu pour les autres.
# Même chose, avec le terme "metal"
tidy_model_beta %>%
filter(term == "metal")
# A tibble: 4 x 3
topic term beta
1 1 metal 2.434275e-02
2 2 metal 5.532748e-37
3 3 metal 5.660067e-36
4 4 metal 3.729133e-31
Quant à "metal", la probabilité la plus élevée revient au topic 1 ! Visualisons les 10 termes qui participent le plus à chaque topic :
tidy_model_beta %>%
group_by(topic) %>%
top_n(10, beta) %>%
ungroup() %>%
arrange(topic, -beta) %>%
ggplot(aes(reorder(term, beta), beta, fill = factor(topic))) +
geom_col(show.legend = FALSE) +
facet_wrap(~ topic, scales = "free") +
scale_fill_viridis_d() +
coord_flip() +
labs(x = "Topic",
y = "beta score",
title = "Topic modeling of 4 wikipedia web pages")
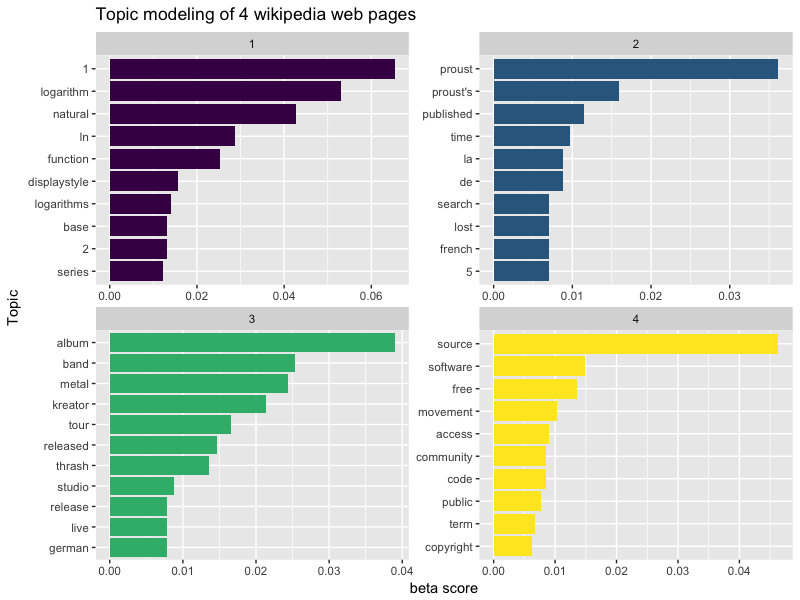Bien, intéressons-nous maintenant à la matrice gamma. Cette dernière contient la probabilité de chaque document d'appartenir à un topic.
tidy_model_gamma <- tidy(lda_model, matrix = "gamma")
tidy_model_gamma
# A tibble: 16 x 3
document topic gamma
1 Open-source model 1 1.592595e-05
2 Natural logarithm 1 3.082349e-05
3 Kreator 1 9.998966e-01
4 Marcel Proust 1 3.123151e-05
5 Open-source model 2 9.999522e-01
6 Natural logarithm 2 3.082349e-05
7 Kreator 2 3.445458e-05
8 Marcel Proust 2 3.123151e-05
9 Open-source model 3 1.592595e-05
10 Natural logarithm 3 3.082349e-05
11 Kreator 3 3.445458e-05
12 Marcel Proust 3 9.999063e-01
13 Open-source model 4 1.592595e-05
14 Natural logarithm 4 9.999075e-01
15 Kreator 4 3.445458e-05
16 Marcel Proust 4 3.123151e-05
# Le topic principal :
tidy_model_gamma %>%
group_by(topic) %>%
arrange(desc(gamma)) %>%
top_n(1)
# A tibble: 4 x 3
# Groups: topic [4]
document topic gamma
1 Open-source model 2 0.9999522
2 Natural logarithm 4 0.9999075
3 Marcel Proust 3 0.9999063
4 Kreator 1 0.9998966
# En le visualisant
tidy_model_gamma %>%
ggplot(aes(document, gamma, fill = factor(topic))) +
geom_col() +
scale_fill_viridis_d() +
coord_flip() +
labs(x = "Corpus",
y = "gamma score",
title = "Topic modeling of 4 wikipedia web pages")
Bon, ici, c'était plutôt facile : nous avions quatre articles très différents, et les résultats sont très tranchés, avec des proba de plus de 99,99 % d'appartenance. Qui plus est, nous avions 1 document pour 1 topic, le décompte était presque trop simple. Car oui, dans la vraie vie, le nombre de documents est plus élevé ; et nous ne chercherons pas forcément à modeler "un topic pour un document" : l'idée était plutôt, ici, d'illustrer le fonctionnement.
Bien, donnons un peu plus de grain à moudre à notre algorithme, et essayons avec 8 articles sur deux thématiques distinctes, autrement dit 4 documents pour 1 topic.
url_list_long <- c("https://en.wikipedia.org/wiki/Kreator",
"https://en.wikipedia.org/wiki/Municipal_Waste_(band)",
"https://en.wikipedia.org/wiki/Havok_(band)",
"https://en.wikipedia.org/wiki/Exodus_(American_band)",
"https://en.wikipedia.org/wiki/Marcel_Proust",
"https://en.wikipedia.org/wiki/Jean-Paul_Sartre",
"https://en.wikipedia.org/wiki/Louis-Ferdinand_C%C3%A9line",
"https://en.wikipedia.org/wiki/Albert_Camus")
data_long <- map_df(.x = url_list_long, .f = scrape_wiki)
dtm_long <- data_long %>%
unnest_tokens(word, text) %>%
count(name, word, sort = TRUE) %>%
anti_join(tidytext::stop_words) %>%
cast_dtm(name, term = word, value = n)
lda_model_long <- LDA(x = dtm_long, k = 2, control = list(seed = 2811))
tidy_model_long_beta <- tidy(lda_model_long, matrix = "beta")
tidy_model_long_beta
# A tibble: 8,386 x 3
topic term beta
1 1 year's 4.156572e-151
2 2 year's 1.575276e-04
3 1 trache 2.901503e-150
4 2 trache 1.575276e-04
5 1 tony 1.992552e-150
6 2 tony 1.575276e-04
7 1 titles 4.143461e-150
8 2 titles 1.575276e-04
9 1 thrashing's 1.072752e-147
10 2 thrashing's 1.575276e-04
# ... with 8,376 more rows
tidy_model_long_beta %>%
group_by(topic) %>%
top_n(10, beta) %>%
ungroup() %>%
arrange(topic, -beta) %>%
ggplot(aes(reorder(term, beta), beta, fill = factor(topic))) +
geom_col(show.legend = FALSE) +
facet_wrap(~ topic, scales = "free") +
scale_fill_viridis_d() +
coord_flip() +
labs(x = "Topic",
y = "beta score",
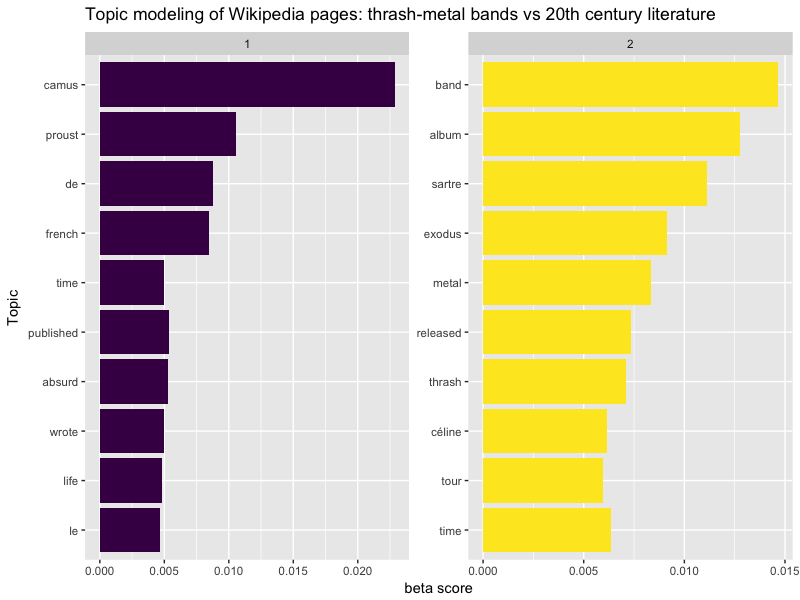
title = "Topic modeling of Wikipedia pages: thrash-metal bands vs 20th century literature")
Et que donne gamma ?
tidy_model_long_gamma <- tidy(lda_model_long, matrix = "gamma")
tidy_model_long_gamma
# A tibble: 16 x 3
document topic gamma
1 Municipal Waste (band) 1 1.365814e-04
2 Marcel Proust 1 9.999618e-01
3 Louis-Ferdinand Céline 1 3.370056e-05
4 Kreator 1 4.216601e-05
5 Jean-Paul Sartre 1 2.206303e-01
6 Havok (band) 1 4.466137e-01
7 Exodus (American band) 1 2.704922e-05
8 Albert Camus 1 9.999793e-01
9 Municipal Waste (band) 2 9.998634e-01
10 Marcel Proust 2 3.822138e-05
11 Louis-Ferdinand Céline 2 9.999663e-01
12 Kreator 2 9.999578e-01
13 Jean-Paul Sartre 2 7.793697e-01
14 Havok (band) 2 5.533863e-01
15 Exodus (American band) 2 9.999730e-01
16 Albert Camus 2 2.073066e-05
# Le topic principal :
tidy_model_long_gamma %>%
group_by(document) %>%
arrange(desc(gamma)) %>%
top_n(1) %>%
arrange(topic)
# A tibble: 8 x 3
# Groups: document [8]
document topic gamma
1 Albert Camus 1 0.9999793
2 Marcel Proust 1 0.9999618
3 Exodus (American band) 2 0.9999730
4 Louis-Ferdinand Céline 2 0.9999663
5 Kreator 2 0.9999578
6 Municipal Waste (band) 2 0.9998634
7 Jean-Paul Sartre 2 0.7793697
8 Havok (band) 2 0.5533863
# En le visualisant
tidy_model_long_gamma %>%
ggplot(aes(document, gamma, fill = factor(topic))) +
geom_col() +
#facet_wrap(~ topic, scales = "free") +
coord_flip() +
scale_fill_viridis_d(name = "Topic") +
labs(x = "Corpus",
y = "gamma score",
title = "Topic modeling of 4 wikipedia web pages")
Intéressant ! On voit ici que l'algorithme ne fait pas un choix tranché pour certaines pages, comme celles de Havok et de Jean Paul Sartre, qui participent chacun à leur échelle aux deux topic.
Que se passe-t-il si nous lui donnons plus de 2 thématiques ?
lda_model_long <- LDA(x = dtm_long, k = 4, control = list(seed = 2811))
tidy_model_long_beta <- tidy(lda_model_long, matrix = "beta")
tidy_model_long_beta
# A tibble: 16,772 x 3
topic term beta
1 1 year's 2.569750e-55
2 2 year's 7.440476e-04
3 3 year's 1.933550e-60
4 4 year's 2.396715e-65
5 1 trache 1.793795e-54
6 2 trache 7.440476e-04
7 3 trache 3.941331e-60
8 4 trache 2.716720e-66
9 1 tony 1.231878e-54
10 2 tony 7.440476e-04
# ... with 16,762 more rows
tidy_model_long_beta %>%
group_by(topic) %>%
top_n(10, beta) %>%
ungroup() %>%
arrange(topic, -beta) %>%
ggplot(aes(reorder(term, beta), beta, fill = factor(topic))) +
geom_col(show.legend = FALSE) +
facet_wrap(~ topic, scales = "free") +
scale_fill_viridis_d() +
coord_flip() +
labs(x = "Topic",
y = "beta score",
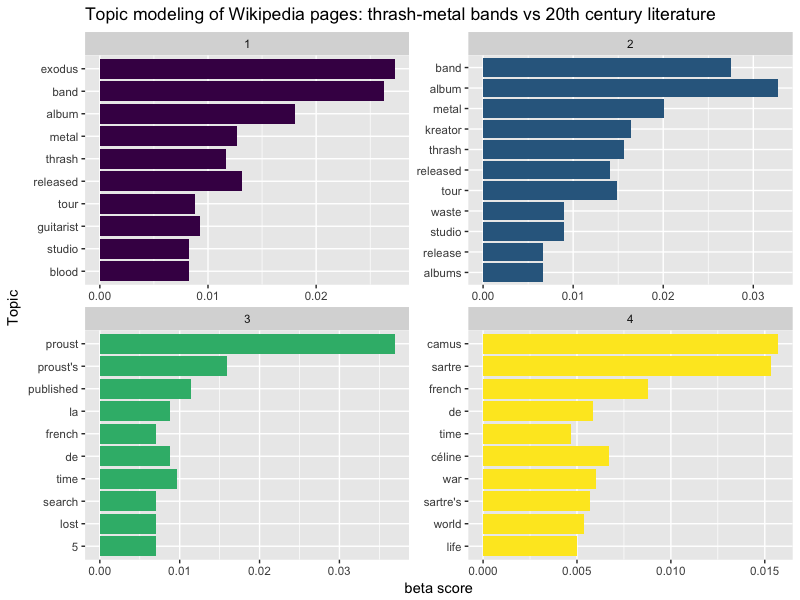
title = "Topic modeling of Wikipedia pages: thrash-metal bands vs 20th century literature")
Et avec gamma ?
tidy_model_long_gamma <- tidy(lda_model_long, matrix = "gamma")
tidy_model_long_gamma
# A tibble: 32 x 3
document topic gamma
1 Municipal Waste (band) 1 8.921420e-05
2 Marcel Proust 1 2.496750e-05
3 Louis-Ferdinand Céline 1 2.201440e-05
4 Kreator 1 2.754419e-05
5 Jean-Paul Sartre 1 1.167548e-05
6 Havok (band) 1 9.998127e-01
7 Exodus (American band) 1 9.999470e-01
8 Albert Camus 1 1.354211e-05
9 Municipal Waste (band) 2 9.997324e-01
10 Marcel Proust 2 2.496750e-05
# ... with 22 more rows
# Le topic principal :
tidy_model_long_gamma %>%
group_by(document) %>%
arrange(desc(gamma)) %>%
top_n(1)
# A tibble: 8 x 3
# Groups: document [8]
document topic gamma
1 Jean-Paul Sartre 4 0.9999650
2 Albert Camus 4 0.9999594
3 Exodus (American band) 1 0.9999470
4 Louis-Ferdinand Céline 4 0.9999340
5 Marcel Proust 3 0.9999251
6 Kreator 2 0.9999174
7 Havok (band) 1 0.9998127
8 Municipal Waste (band) 2 0.9997324
# En le visualisant
tidy_model_long_gamma %>%
ggplot(aes(document, gamma, fill = factor(topic))) +
geom_col() +
coord_flip() +
scale_fill_viridis_d() +
labs(x = "Corpus",
y = "gamma score",
title = "Topic modeling of 4 wikipedia web pages")
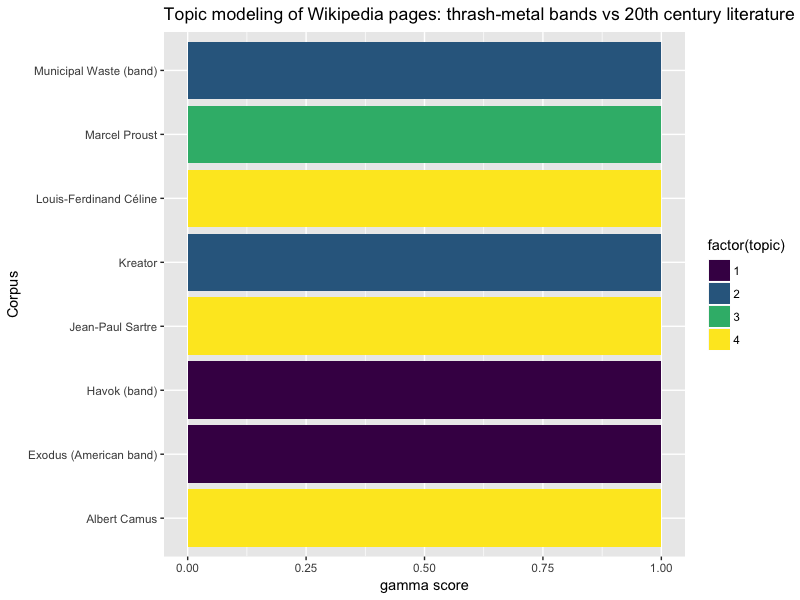Ici, le découpage est un peu plus net ! Passons maintenant à une plus grosse échelle.
Un dernier pour la route ?
Bon, donnons lui encore plus à manger, avec un corpus plus volumineux, et avec des contenus qui seront plus similaires : si on comparait des lyrics de Kreator, Motörhead, Pantera et Iron Maiden ?
## Une fonction pour scraper et créer un df depuis metrolyrics.com
scrape_lyrics_url <- function(url){
url <- read_html(url)
df <- tibble(text =url %>% html_nodes(".songs-table") %>% html_nodes("a") %>% html_attr("href"),
name = url %>% html_nodes("h1") %>% html_text())
return(df)
}
scrape_lyrics_page <- function(url){
url <- read_html(url)
df <- tibble(text = url %>% html_nodes("#lyrics-body-text") %>% html_text(),
band = url %>% html_nodes("h2") %>% html_nodes("a") %>% html_text(),
song = url %>% html_nodes("h1") %>% html_text())
df$song <- gsub(pattern = " Lyrics", "", df$song)
return(df)
}
song_index <- c("http://www.metrolyrics.com/kreator-lyrics.html",
"http://www.metrolyrics.com/kreator-alpage-2.html",
"http://www.metrolyrics.com/kreator-alpage-3.html",
"http://www.metrolyrics.com/iron-maiden-lyrics.html",
"http://www.metrolyrics.com/iron-maiden-alpage-2.html",
"http://www.metrolyrics.com/iron-maiden-alpage-3.html",
"http://www.metrolyrics.com/motrhead-lyrics.html",
"http://www.metrolyrics.com/motrhead-alpage-2.html",
"http://www.metrolyrics.com/motrhead-alpage-3.html",
"http://www.metrolyrics.com/pantera-lyrics.html",
"http://www.metrolyrics.com/pantera-alpage-2.html")
url_list <- map_df(song_index, scrape_lyrics_url)
data_m <- map_df(.x = url_list$text, .f = scrape_lyrics_page)
dim(data_m)
[1] 698 3
Nous voilà donc avec 698 morceaux, soit 698 documents. Pour mettre l'algorithme à l'épreuve, nous allons lui fournir un corpus avec juste les chansons, et lui demander de les classer en quatre thèmes. En clair, imaginons que nous ayons perdu la colonne contenant le nom des groupes, et que nous tentions de les retrouver en les classant par topic.
Une fois notre test fait, nous vérifierons en croisant avec le nom des groupes, afin de voir si les topics se fondent avec les groupes.
dtm_m <- data_m %>%
unnest_tokens(word, text) %>%
count(song, word, sort = TRUE) %>%
anti_join(tidytext::stop_words) %>%
cast_dtm(song, term = word, value = n)
lda_model_m <- LDA(x = dtm_m, k = 4, control = list(seed = 2811))
tidy_model_m_beta <- tidy(lda_model_m, matrix = "beta")
tidy_model_m_beta
# A tibble: 31,672 x 3
topic term beta
1 1 riotevery 5.307780e-143
2 2 riotevery 1.211671e-10
3 3 riotevery 5.992365e-05
4 4 riotevery 2.273045e-144
5 1 riotall 1.608980e-142
6 2 riotall 1.284382e-10
7 3 riotall 5.992364e-05
8 4 riotall 2.341197e-144
9 1 patriots 1.807062e-142
10 2 patriots 2.247364e-10
# ... with 31,662 more rows
tidy_model_m_beta %>%
group_by(topic) %>%
top_n(10, beta) %>%
ungroup() %>%
arrange(topic, -beta) %>%
ggplot(aes(reorder(term, beta), beta, fill = factor(topic))) +
geom_col(show.legend = FALSE) +
facet_wrap(~ topic, scales = "free") +
scale_fill_viridis_d() +
coord_flip() +
labs(x = "Topic",
y = "beta score",
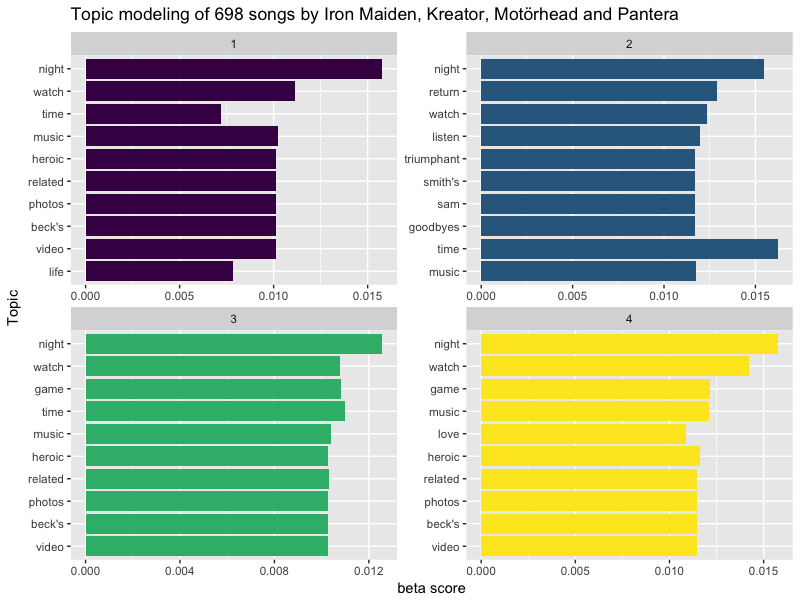
title = "Topic modeling of 698 songs by Iron Maiden, Kreator, Motörhead and Pantera")
Ici, la matrice gamma contenue dans notre modèle va nous donner la participation de chaque morceau aux différents topics. Ce que nous voulons, c'est connaître la participation de chaque groupe à chaque topic. C'est pourquoi nous devons commencer par recréer le tableau avec les noms des bands.
tidy_model_m_gamma <- tidy(lda_model_m, matrix = "gamma")
tidy_model_m_gamma <- tidy_model_m_gamma %>%
rename(song = document) %>%
left_join(data_m, by = "song") %>%
select(topic, gamma, band, song)
tidy_model_m_gamma
# A tibble: 2,792 x 4
topic gamma band song
1 1 0.0005307050 Kreator Zero To None
2 1 0.0005456218 Pantera You've Got To Be Belong To It
3 1 0.0005614014 Pantera You've Got To Belong To It
4 1 0.0002268342 Kreator World War Now
5 1 0.0004843583 Kreator WORLD BEYOND
6 1 0.0003400971 Iron Maiden Women in Uniform
7 1 0.0003876368 Kreator Winter Martyrium
8 1 0.0006563044 Iron Maiden Wildest Dreams
9 1 0.9984904258 Iron Maiden Where Eagles Dare
10 1 0.0005456218 Iron Maiden When Two Worlds Collide
# ... with 2,782 more rows
# En le visualisant
tidy_model_m_gamma %>%
ggplot(aes(band, gamma)) +
geom_boxplot(show.legend = FALSE) +
facet_wrap(~ topic, scales = "free") +
coord_flip() +
labs(x = "Corpus",
y = "gamma score",
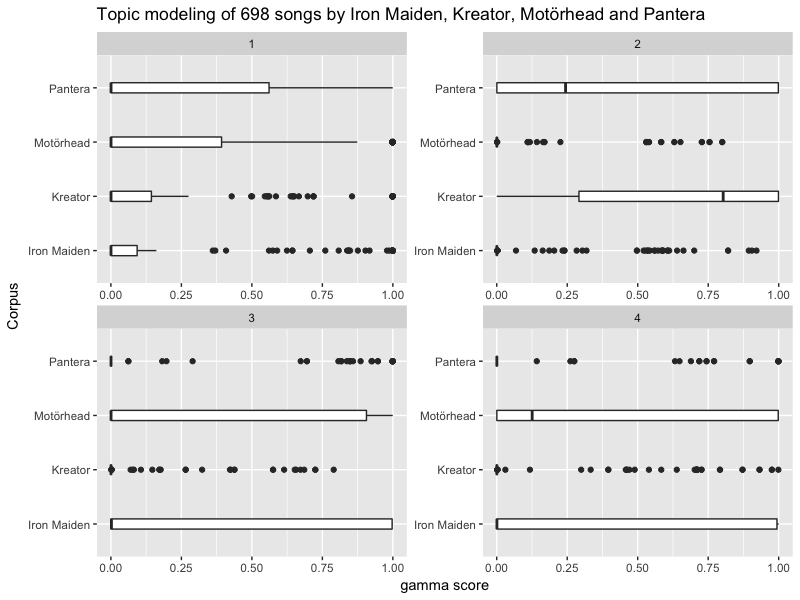
title = "Topic modeling of 698 songs by Iron Maiden, Kreator, Motörhead and Pantera")
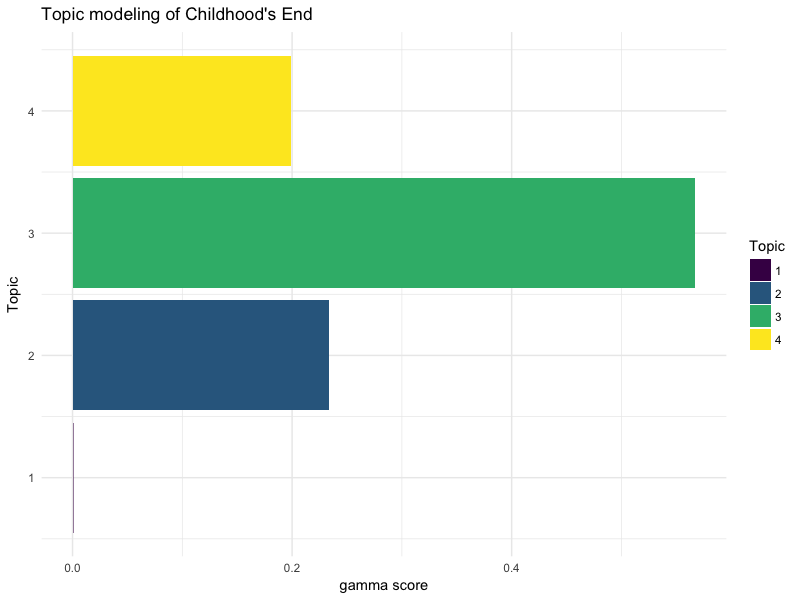
Ici, notre modèle ne permet pas de déterminer quel groupe génère quel topic. En effet, chaque morceau génère un pourcentage de participation à plusieurs topics. Par exemple, la chanson "Childhood's End" de Iron Maiden apparaît sur 3 des 4 topic :
tidy_model_m_gamma %>%
filter(song == "Childhood's End") %>%
ggplot(aes(topic, gamma, fill = factor(topic))) +
geom_col() +
#facet_wrap(~ factor(topic), scales = "free") +
scale_fill_viridis_d(name = "Topic") +
coord_flip() +
labs(x = "Topic",
y = "gamma score",
title = "Topic modeling of Childhood's End ") +
theme_minimal()
Pour nous représenter plus globalement ce classement, nous pouvons regarder du côté de tous les scores gamma :
tidy_model_m_gamma %>%
ggplot(aes(gamma)) +
geom_histogram(bins = 100) +
scale_y_log10() +
labs(x = "Gamma score",
y = "Count",
title = "Gamma score in metal songs topic modeling") +
theme_minimal()
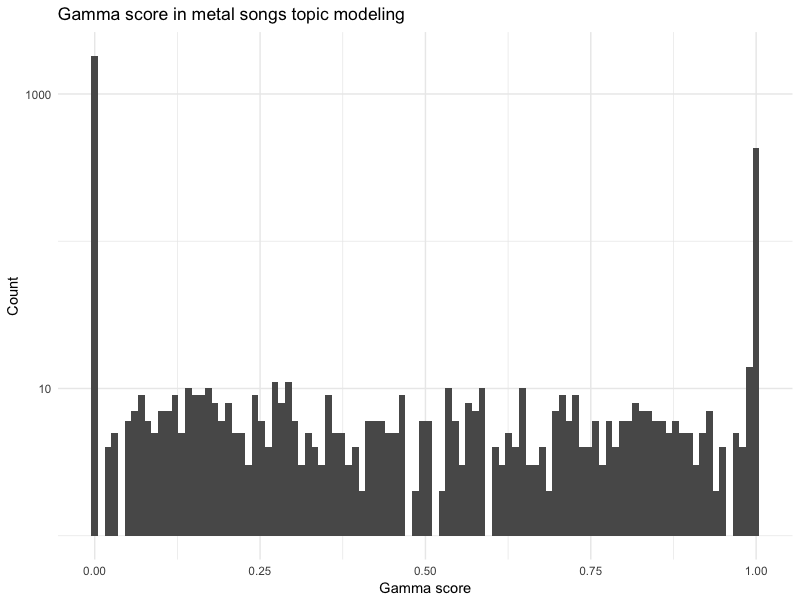Comment lire ce graphique ? Lorsqu'un topic model offre un découpage bien tranché, les deux modes sont autour de 0 et de 1. En effet, un document classé de manière nette dans 4 topics va afficher des scores gamma, par exemple, de 0.99 / 0.001 / 0.002 / 0.007. Un document "mal classé" va plutôt afficher des scores de 0.30 / 0.20 / 0.25 / 0.25. Vous avez compris l'idée 🙂
Bien, mais alors, quel intérêt de ce topic modeling s'il n'est pas tranché ? Eh bien, imaginons que vous soyez un moteur de recherche (très (très)) rudimentaire qui conseille des chansons, par similarité de parole. Vous pourriez simplement proposer de filtrer les chansons avec du topic modeling :
chanson_de_depart <- "Where Eagles Dare"
conseil <- function(chanson) {
topic <- filter(tidy_model_m_gamma, song == chanson) %>%
pull(topic)
filter(tidy_model_m_gamma, topic == topic) %>%
arrange(desc(gamma)) %>%
unique() %>%
slice(1:5) %>%
select(band, song)
}
conseil("Where Eagles Dare")
# A tibble: 5 x 2
band song
1 Iron Maiden Rime of The Ancient Mariner
2 Iron Maiden The Book Of Souls
3 Kreator Replicas Of Life
4 Iron Maiden The Legacy
5 Pantera Shedding Skin
conseil("Hordes of Chaos")
A tibble: 5 x 2
band song
1 Iron Maiden Rime of The Ancient Mariner
2 Iron Maiden The Book Of Souls
3 Kreator Replicas Of Life
4 Iron Maiden The Legacy
5 Pantera Shedding Skin
Alors, ça ne vous donne pas envie de vous lancer dans le text-mining ? Parfait, vous êtes prêt à en parler 😉
Source :
+ Text Mining with R
+ Learning Social Media Analytics with
+ Online Inference of Topics with Latent Dirichlet Allocation
[…] I also compute the tf_idf and I am grateful toThinkR blog post on that, which you can read here.It’s in French though, but the idea of the blog post is to present topic modeling with […]