Bienvenue à toi, ô cher utilisateur de SAS qui souhaite s’ouvrir à de nouveaux horizons ! Nous commençons avec cet article une nouvelle micro série de publications dédiées aux adeptes de SAS passant à R. Si tu ne jures que par les PROC mais que pour une raison x ou y R s’impose à toi : pas de panique, tu es au bon endroit. Et on va entamer cette série en douceur, avec le calcul d’indices statistiques simples.
Sommaire
Importer des données SAS dans R
Avant toute chose, j’imagine que si tu as l’habitude de travailler avec SAS, tu as des données SAS que tu souhaites pouvoir importer dans R. Pour importer une table SAS au format sas7bdat, plusieurs fonctions sont possibles :
- La fonction
read_sas()du package{heaven}:
# intallation et import du package
install.packages("haven")
library(haven)
# import des donnees
data <- read_sas("airline.sas7bdat")- la fonction
read.sas7bdat()du package{sas7bdat}:
# intallation et import du package
install.packages("sas7bdat")
library(sas7bdat)
# import des donnees
data <- read.sas7bdat("airline.sas7bdat")- si tu as un fichier au format SAS XPORT, la fonction
read.xport()du package{foreign}importera les données :
# intallation et import du package
install.packages("foreign")
library(foreign)
# import des donnees
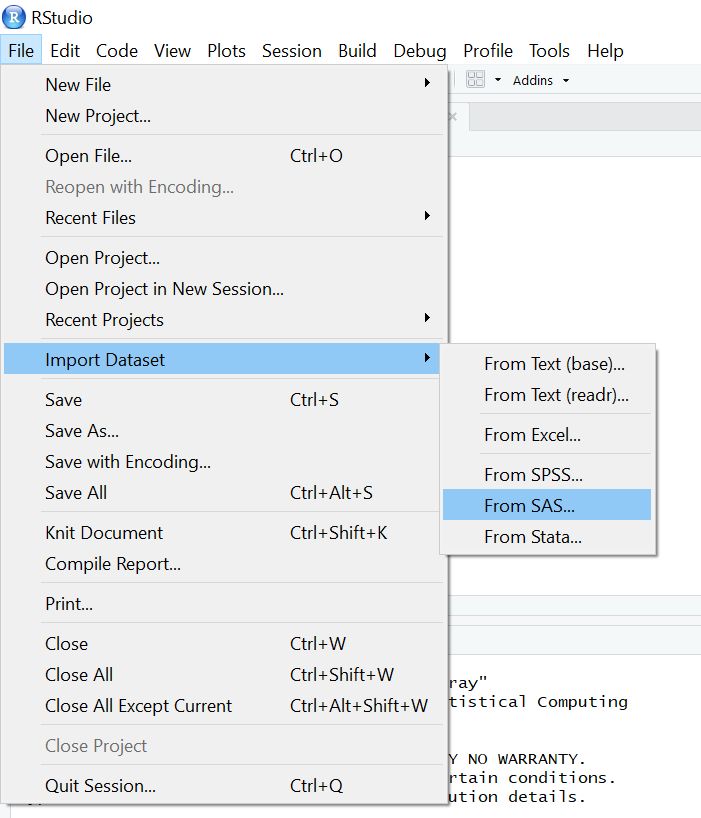
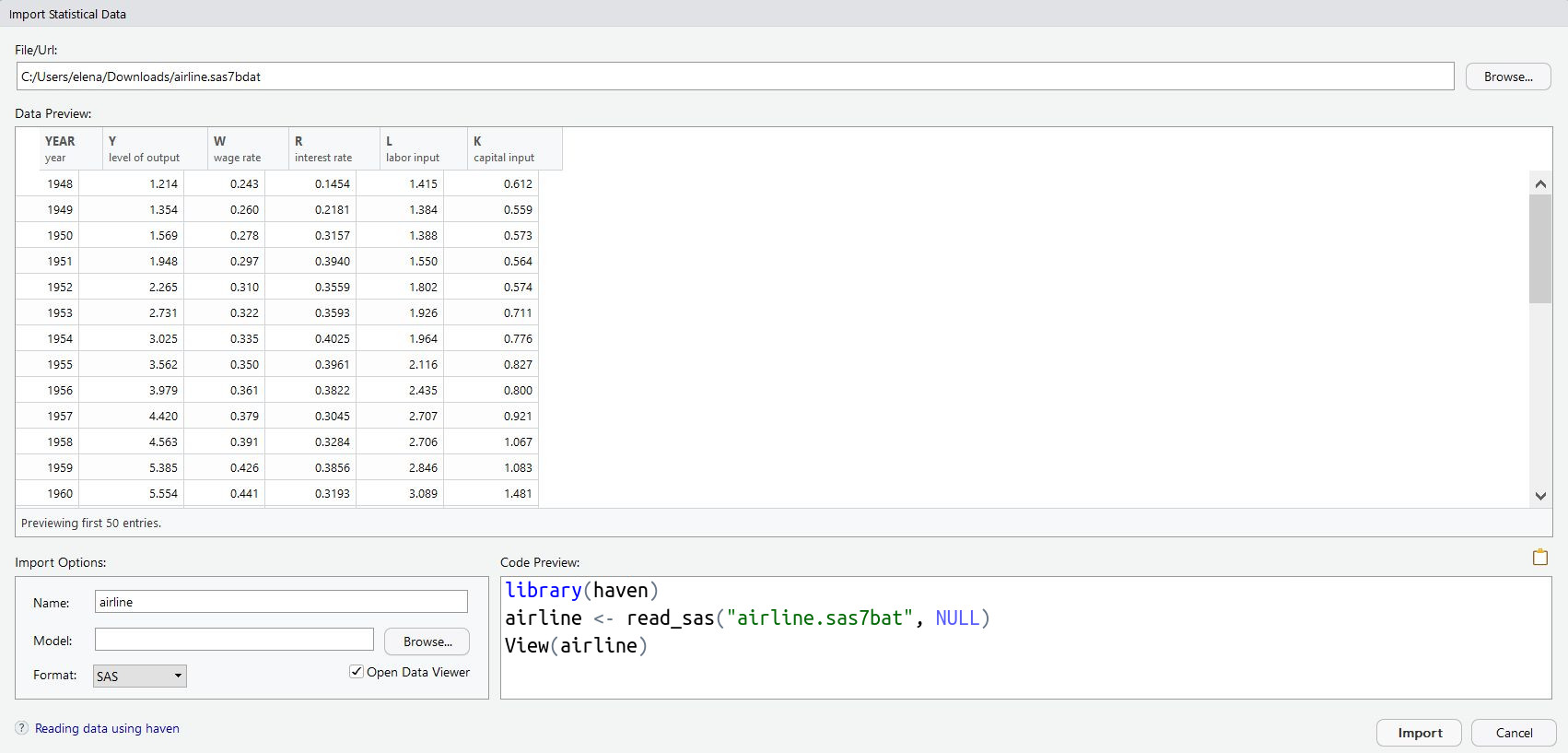
data <- read.xport("airline.xpt")Vous pouvez également passer par l’interface de Rstudio : File > Import Dataset > From SAS :
PROC MEANS / PROC SUMMARY – en SAS
Ces deux PROC permettent la même chose : déterminer les statistiques de base d’un jeu de données. L’unique différence réside en la sortie de la PROC : la procédure MEANS édite par défaut toutes les statistiques demandées, contrairement à la procédure SUMMARY pour laquelle l’option NO PRINT est sélectionnée. Dans la suite de l’article, nous allons donc nous concentrer sur une seule de ces deux procédures : PROC MEANS.
Regardons plus en détail cette procédure :
PROC MEANS DATA=nomtab_input optnum;
VAR var1 var2 var3 var4 var5 var6 ;
CLASS var2 ...;
WEIGHT var3;
ID var4;
FREQ var5 ... ;
BY var7 ...;
OUTPUT OUT=nomtab_output optnum=var ;DATA désigne le nom de la table d’entrée. optnum représente ici les indicateurs statistiques disponibles sous SAS :
- N : nombre d’observations. Si des classes sont spécifiées par l’instruction CLASS ou BY, N est le nombre d’observations par classe.
- NMISS : nombre d’observations manquantes pour chaque variable
- MAXDEC=n : nombre de chiffres (de 0 à 8) à retenir après la virgule (par défaut, n=2)
- MISSING : les valeurs manquantes des variables données dans l’instruction CLASS constituent une classe
- MEAN : moyenne empirique de chaque variable numérique
- STD : écart-type de chaque variable numérique
- MIN : minimum de chaque variable numérique
- MAX : maximum de chaque variable numérique
- RANGE : étendue de chaque variable numérique
- SUM : somme de chaque variable numérique
- VAR : variance de chaque variable numérique
- USS : somme des carrés de chaque variable numérique
- CSS : somme des carrés des écarts à la moyenne de chaque variable numérique
- STDERR : écart-type moyen de chaque variable numérique
- CV : coefficient de variation (STD/MEAN) de chaque variable numérique
- SKEWNESS : coefficient d’asymétrie de chaque variable numérique
- KURTOSIS détermine le coefficient d’aplatissement de chaque variable numérique
- T : T de Student associé à chaque variable numérique
- PRT : probabilité d’obtention d’une valeur supérieure à T sous l’hypothèse de moyenne nulle de la variable numérique
Les instructions, pour les deux procédures, sont les suivantes :
- VAR : c’est la liste des variables de la table
nomtab_inputque l’on retient. Si on ne spécifie pas cette instruction, toutes les variables seront retenues par défaut. - CLASS : les calculs sont réalisés par classe de variables (ici, var1, factorille) triées a priori.
- WEIGHT : si on a une variable de pondération.
- ID : variable d’id. Si elle n’est pas spécifiée, l’id est le numéro de ligne.
- FREQ : estime en pourcentages, simples et cumulés, les variables citées.
- BY : les calculs sont réalisés par classe de variables. Si on utilise au préalable la procédure de tri PROC SORT, les résultats seront identiques à ceux obtenus avec l’instruction CLASS.
- OUTPUT OUT=nomtab_output optnum=var spécifie le nom de la table de sortie contenant les divers indicateurs statistiques, et var désigne une ou plusieurs des variables retenues dans l’instruction VAR.
Source : https://support.sas.com/documentation/cdl/en/proc/61895/HTML/default/viewer.htm#a002473330.htm
PROC MEANS / PROC SUMMARY – traduction en R
La question qui se pose maintenant est : peut-on faire la même chose avec R ? Evidemment, la réponse est : OUI ! Plusieurs fonctions sont dédiées à la statistique descriptive et au calcul des indicateurs donnés ci-dessus.
{base}
La fonction summary() de R {base} est la plus fréquemment utilisée. Elle permet d’obtenir :
- le minimum, le maximum, les premier et troisième quartiles, la médiane et la moyenne de chaque variable numérique
- le nombre d’observations par classe pour les variables factorielles
- le nombre de valeurs manquantes pour chaque variable
Il est possible de spécifier le nombre de chiffres à afficher grâce au paramètre digits.
summary(iris, digits = 5)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.3000 Min. :2.0000 Min. :1.000 Min. :0.1000 setosa :50
## 1st Qu.:5.1000 1st Qu.:2.8000 1st Qu.:1.600 1st Qu.:0.3000 versicolor:50
## Median :5.8000 Median :3.0000 Median :4.350 Median :1.3000 virginica :50
## Mean :5.8433 Mean :3.0573 Mean :3.758 Mean :1.1993
## 3rd Qu.:6.4000 3rd Qu.:3.3000 3rd Qu.:5.100 3rd Qu.:1.8000
## Max. :7.9000 Max. :4.4000 Max. :6.900 Max. :2.5000{Hmisc}
Nous pouvons également citer la fonction describe() du package {Hmisc}. Elle renvoie une liste dont chaque élément correspond à une variable. Elle permet d’obtenir :
- le nombre de variables et de nombre d’observations de la table
- le nombre d’observations, le nombre de valeurs manquantes et le nombre de valeurs distinctes pour chaque variable
- la moyenne, la différence moyenne de Gini et les quantiles à 5%, 10%, 25%, 50%, 75%, 90% et 95% pour les variables numériques, ainsi que les 5 plus petites et les 5 plus grandes observations
- la fréquence et la proportion de chaque catégorie pour les variables factorielles
library(Hmisc)
Hmisc::describe(iris, digits = 5)## iris
##
## 5 Variables 150 Observations
## --------------------------------------------------------------------------------------
## Sepal.Length
## n missing distinct Info Mean Gmd .05 .10 .25
## 150 0 35 0.998 5.8433 0.94619 4.600 4.800 5.100
## .50 .75 .90 .95
## 5.800 6.400 6.900 7.255
##
## lowest : 4.3 4.4 4.5 4.6 4.7, highest: 7.3 7.4 7.6 7.7 7.9
## --------------------------------------------------------------------------------------
## Sepal.Width
## n missing distinct Info Mean Gmd .05 .10 .25
## 150 0 23 0.992 3.0573 0.48723 2.345 2.500 2.800
## .50 .75 .90 .95
## 3.000 3.300 3.610 3.800
##
## lowest : 2.0 2.2 2.3 2.4 2.5, highest: 3.9 4.0 4.1 4.2 4.4
## --------------------------------------------------------------------------------------
## Petal.Length
## n missing distinct Info Mean Gmd .05 .10 .25
## 150 0 43 0.998 3.758 1.9785 1.30 1.40 1.60
## .50 .75 .90 .95
## 4.35 5.10 5.80 6.10
##
## lowest : 1.0 1.1 1.2 1.3 1.4, highest: 6.3 6.4 6.6 6.7 6.9
## --------------------------------------------------------------------------------------
## Petal.Width
## n missing distinct Info Mean Gmd .05 .10 .25
## 150 0 22 0.99 1.1993 0.86755 0.2 0.2 0.3
## .50 .75 .90 .95
## 1.3 1.8 2.2 2.3
##
## lowest : 0.1 0.2 0.3 0.4 0.5, highest: 2.1 2.2 2.3 2.4 2.5
## --------------------------------------------------------------------------------------
## Species
## n missing distinct
## 150 0 3
##
## Value setosa versicolor virginica
## Frequency 50 50 50
## Proportion 0.333 0.333 0.333
## --------------------------------------------------------------------------------------{pastecs}
Autre fonction qui peut être utile : la fonction stat.desc() du package {pastecs}, qui renvoie pour chaque variable numérique : le nombre de valeurs, le nombre de NULL, le nombre de NA, les valeurs minimale et maximale, le range, la somme, la médiane, la moyenne, l’erreur standard, l’intervalle de confiance de la moyenne, la variance, l’écart-type, et le coefficient de variation.
library(pastecs)
stat.desc(iris)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## nbr.val 150.00000000 150.00000000 150.0000000 150.00000000 NA
## nbr.null 0.00000000 0.00000000 0.0000000 0.00000000 NA
## nbr.na 0.00000000 0.00000000 0.0000000 0.00000000 NA
## min 4.30000000 2.00000000 1.0000000 0.10000000 NA
## max 7.90000000 4.40000000 6.9000000 2.50000000 NA
## range 3.60000000 2.40000000 5.9000000 2.40000000 NA
## sum 876.50000000 458.60000000 563.7000000 179.90000000 NA
## median 5.80000000 3.00000000 4.3500000 1.30000000 NA
## mean 5.84333333 3.05733333 3.7580000 1.19933333 NA
## SE.mean 0.06761132 0.03558833 0.1441360 0.06223645 NA
## CI.mean.0.95 0.13360085 0.07032302 0.2848146 0.12298004 NA
## var 0.68569351 0.18997942 3.1162779 0.58100626 NA
## std.dev 0.82806613 0.43586628 1.7652982 0.76223767 NA
## coef.var 0.14171126 0.14256420 0.4697441 0.63555114 NA{skimr}
Une autre fonction intéressante : la fonction skim() du package {skimr}, qui renvoie
- le nombre de lignes et de colonnes du jeu de données, les types de variables, le nombre de valeurs manquantes pour chaque variable
- pour les variables factorielles : si elles sont ordonnées ou non, le nombre de valeurs uniques, la fréquence de chaque modalité
- pour les variables numériques : la moyenne, l’écart-type, les quantiles à p = 0, 25, 50, 75, 100, et un histogramme
library(skimr)
skim(iris)| Name | iris |
| Number of rows | 150 |
| Number of columns | 5 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 4 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| Species | 0 | 1 | FALSE | 3 | set: 50, ver: 50, vir: 50 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| Sepal.Length | 0 | 1 | 5.84 | 0.83 | 4.3 | 5.1 | 5.80 | 6.4 | 7.9 | ▆▇▇▅▂ |
| Sepal.Width | 0 | 1 | 3.06 | 0.44 | 2.0 | 2.8 | 3.00 | 3.3 | 4.4 | ▁▆▇▂▁ |
| Petal.Length | 0 | 1 | 3.76 | 1.77 | 1.0 | 1.6 | 4.35 | 5.1 | 6.9 | ▇▁▆▇▂ |
| Petal.Width | 0 | 1 | 1.20 | 0.76 | 0.1 | 0.3 | 1.30 | 1.8 | 2.5 | ▇▁▇▅▃ |
La fonction skim() est compatible avec les verbes de manipulation de données du tidyverse et de {dplyr} et permet également de calculer ces statistiques de base par classe :
iris %>%
dplyr::group_by(Species) %>%
skim()| Name | Piped data |
| Number of rows | 150 |
| Number of columns | 5 |
| _______________________ | |
| Column type frequency: | |
| numeric | 4 |
| ________________________ | |
| Group variables | Species |
Variable type: numeric
| skim_variable | Species | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Sepal.Length | setosa | 0 | 1 | 5.01 | 0.35 | 4.3 | 4.80 | 5.00 | 5.20 | 5.8 | ▃▃▇▅▁ |
| Sepal.Length | versicolor | 0 | 1 | 5.94 | 0.52 | 4.9 | 5.60 | 5.90 | 6.30 | 7.0 | ▂▇▆▃▃ |
| Sepal.Length | virginica | 0 | 1 | 6.59 | 0.64 | 4.9 | 6.23 | 6.50 | 6.90 | 7.9 | ▁▃▇▃▂ |
| Sepal.Width | setosa | 0 | 1 | 3.43 | 0.38 | 2.3 | 3.20 | 3.40 | 3.68 | 4.4 | ▁▃▇▅▂ |
| Sepal.Width | versicolor | 0 | 1 | 2.77 | 0.31 | 2.0 | 2.52 | 2.80 | 3.00 | 3.4 | ▁▅▆▇▂ |
| Sepal.Width | virginica | 0 | 1 | 2.97 | 0.32 | 2.2 | 2.80 | 3.00 | 3.18 | 3.8 | ▂▆▇▅▁ |
| Petal.Length | setosa | 0 | 1 | 1.46 | 0.17 | 1.0 | 1.40 | 1.50 | 1.58 | 1.9 | ▁▃▇▃▁ |
| Petal.Length | versicolor | 0 | 1 | 4.26 | 0.47 | 3.0 | 4.00 | 4.35 | 4.60 | 5.1 | ▂▂▇▇▆ |
| Petal.Length | virginica | 0 | 1 | 5.55 | 0.55 | 4.5 | 5.10 | 5.55 | 5.88 | 6.9 | ▃▇▇▃▂ |
| Petal.Width | setosa | 0 | 1 | 0.25 | 0.11 | 0.1 | 0.20 | 0.20 | 0.30 | 0.6 | ▇▂▂▁▁ |
| Petal.Width | versicolor | 0 | 1 | 1.33 | 0.20 | 1.0 | 1.20 | 1.30 | 1.50 | 1.8 | ▅▇▃▆▁ |
| Petal.Width | virginica | 0 | 1 | 2.03 | 0.27 | 1.4 | 1.80 | 2.00 | 2.30 | 2.5 | ▂▇▆▅▇ |
{psych}
Le package {psych} offre également des fonctions utiles comme la fonction describe(), avec également la possibilité de calculer des statistiques de base par groupe grâce à la fonction describeBy(). Elle renvoie, pour les variables numériques : la moyenne, l’écart-type, la médiane, la moyenne ajustée (avec trim = 0.1 par défaut), l’écart médian absolu, le minimum, le maximum, skew – le coefficient d’asymétrie, kurtosis -qui détermine le coefficient d’aplatissement de la variable, et l’erreur standard.
library(psych)
describeBy(iris, group = "Species")##
## Descriptive statistics by group
## group: setosa
## vars n mean sd median trimmed mad min max range skew kurtosis se
## Sepal.Length 1 50 5.01 0.35 5.0 5.00 0.30 4.3 5.8 1.5 0.11 -0.45 0.05
## Sepal.Width 2 50 3.43 0.38 3.4 3.42 0.37 2.3 4.4 2.1 0.04 0.60 0.05
## Petal.Length 3 50 1.46 0.17 1.5 1.46 0.15 1.0 1.9 0.9 0.10 0.65 0.02
## Petal.Width 4 50 0.25 0.11 0.2 0.24 0.00 0.1 0.6 0.5 1.18 1.26 0.01
## Species* 5 50 1.00 0.00 1.0 1.00 0.00 1.0 1.0 0.0 NaN NaN 0.00
## ----------------------------------------------------------------
## group: versicolor
## vars n mean sd median trimmed mad min max range skew kurtosis se
## Sepal.Length 1 50 5.94 0.52 5.90 5.94 0.52 4.9 7.0 2.1 0.10 -0.69 0.07
## Sepal.Width 2 50 2.77 0.31 2.80 2.78 0.30 2.0 3.4 1.4 -0.34 -0.55 0.04
## Petal.Length 3 50 4.26 0.47 4.35 4.29 0.52 3.0 5.1 2.1 -0.57 -0.19 0.07
## Petal.Width 4 50 1.33 0.20 1.30 1.32 0.22 1.0 1.8 0.8 -0.03 -0.59 0.03
## Species* 5 50 2.00 0.00 2.00 2.00 0.00 2.0 2.0 0.0 NaN NaN 0.00
## ----------------------------------------------------------------
## group: virginica
## vars n mean sd median trimmed mad min max range skew kurtosis se
## Sepal.Length 1 50 6.59 0.64 6.50 6.57 0.59 4.9 7.9 3.0 0.11 -0.20 0.09
## Sepal.Width 2 50 2.97 0.32 3.00 2.96 0.30 2.2 3.8 1.6 0.34 0.38 0.05
## Petal.Length 3 50 5.55 0.55 5.55 5.51 0.67 4.5 6.9 2.4 0.52 -0.37 0.08
## Petal.Width 4 50 2.03 0.27 2.00 2.03 0.30 1.4 2.5 1.1 -0.12 -0.75 0.04
## Species* 5 50 3.00 0.00 3.00 3.00 0.00 3.0 3.0 0.0 NaN NaN 0.00{doBy}
Enfin, la fonction summaryBy() du package {doBy} permet de fournir une grande partie des indicateurs donnés par la PROC SUMMARY de SAS :
library(doBy)
fun_sum <- function(x) {
c(N = length(x), NMISS = length(which(is.na(x))), MEAN = mean(x, na.rm = TRUE), STD = sd(x, na.rm = TRUE),
MIN = min(x, na.rm = TRUE), MAX = max(x, na.rm = TRUE), RANGE = range(x, na.rm = TRUE),
SUM = sum(x, na.rm = TRUE), VAR = var(x, na.rm = TRUE), USS = sum(x^2, na.rm = TRUE),
CSS = sum((x - mean(x, na.rm = TRUE))^2, na.rm = TRUE),
CV = sd(x, na.rm = TRUE)/mean(x, na.rm = TRUE), SKEWNESS = e1071::skewness(x, na.rm = TRUE),
KURTOSIS = e1071::kurtosis(x, na.rm = TRUE), T = t.test(x))
}
summaryBy(. ~ Species, data = iris, FUN = fun_sum)En résumé, il n’y a pas vraiment de fonction dans R qui reproduise trait pour trait les PROC de SAS, la raison en est sûrement que les personnes ayant trouvé les fonctions natives peu satisfaisantes ont sculpté une solution qui réponde à leurs propres besoins. Et l’ont rendue open source !
Et vous, y trouvez-vous votre compte avec les packages et fonctions proposées ou allez-vous construire les votres ?
Dans le prochain épisode…
Nous vous parlerons de l’étape DATA et de la PROC SQL très prochainement, alors soyez attentifs à nos prochaines publications !
Dans la série : « Migration de SAS vers R » :
En attendant, vous pouvez continuer à vous familiariser avec R grâce à nos articles précédents :
- Si vous êtes familiarisés avec Excel, vous trouverez ici quelques correspondances entre Excel et R : https://thinkr.fr/comparaison-entre-excel-et-r-analyses-statistiques-et-graphiques/
- Si vous voulez en savoir plus sur les graphiques en R : https://thinkr.fr/il-ny-a-pas-que-ggplot-dans-la-vie/




Laisser un commentaire