Vous avez fait votre expérience ou votre enquête, ou vous avez récupéré des données et vous êtes prêts à les analyser. Quelle est la première étape ? Tout le monde vous répondra qu’il faut les visualiser, oui, d’accord, mais comment ? et pourquoi ? Quels sont les pièges à éviter ?

La représentation des données

Représenter ses données avant de les analyser c’est important. Cela permet de mieux les connaître, d’identifier les tendances et les potentiels effets. Vous pourrez chercher les valeurs extrêmes et/ou aberrantes pour décider de les retirer ou les conserver selon votre question. Vous pourrez ensuite choisir les analyses statistiques appropriées. En effet, en fonction du type de données (binaire, linéaire, quadratique, bimodal, …) vous ne réaliserez pas les mêmes analyses.

Sur le blog de ThinkR, une fois que vous savez faire un beau jeu de données avec « Les dix commandements d’une base de données réussie », on vous parle des représentations graphiques. Par exemple : “Il n’y a pas que ggplot dans la vie” ou “Guide de survie ggplot2 à destination des datajournalistes (et des autres aussi)”. Alors pourquoi vous proposer un nouveau post sur le sujet ?
Cela part d’un constat : oui, c’est bien de représenter ses données dans de beaux graphiques, encore faut-il qu’ils soient pertinents… 😓 Le diagramme en barres ou barplot est le graphique préféré des scientifiques, voyons ce qu’il cache !

L’exemple à ne pas faire

Le bar-barplot

Imaginons que votre jeu de données soit les tailles de deux groupes d’individus (le code qui crée ce jeu de données est présent à la fin de l’article pour ne pas vous spoiler dès le début).
Nous avons envie de savoir la taille des individus est différente entre les deux groupes. Pour comparer deux populations, on vous a probablement appris à regarder la moyenne et l’écart-type. Vous décidez donc de faire un graphique en barres pour représenter la moyenne, avec une barre d’erreur pour l’écart-type. Ce graphique est communément appelé un “barbarplot”.
Vous l’avez vu dans “Utiliser la grammaire dplyr pour triturer ses données”, pour calculer une variable résumée (ici moyenne et ecart-type) séparément pour des groupes différents, nous utilisons la combinaison group_by + summarise.

library(tidyverse)
info <- data %>%
  group_by(Groupe) %>%
  summarise(Moyenne = mean(Taille),
            Ecart = sd(Taille))
ggplot(info, aes(x = Groupe, y = Moyenne, fill = Groupe)) +
  geom_bar(stat = "identity", position = position_dodge(),
           colour = "grey30") +
  geom_errorbar(
    aes(ymin = Moyenne - Ecart, ymax = Moyenne + Ecart),
    width = .2, position = position_dodge(.9), size = 1
  ) + 
  scale_fill_viridis_d()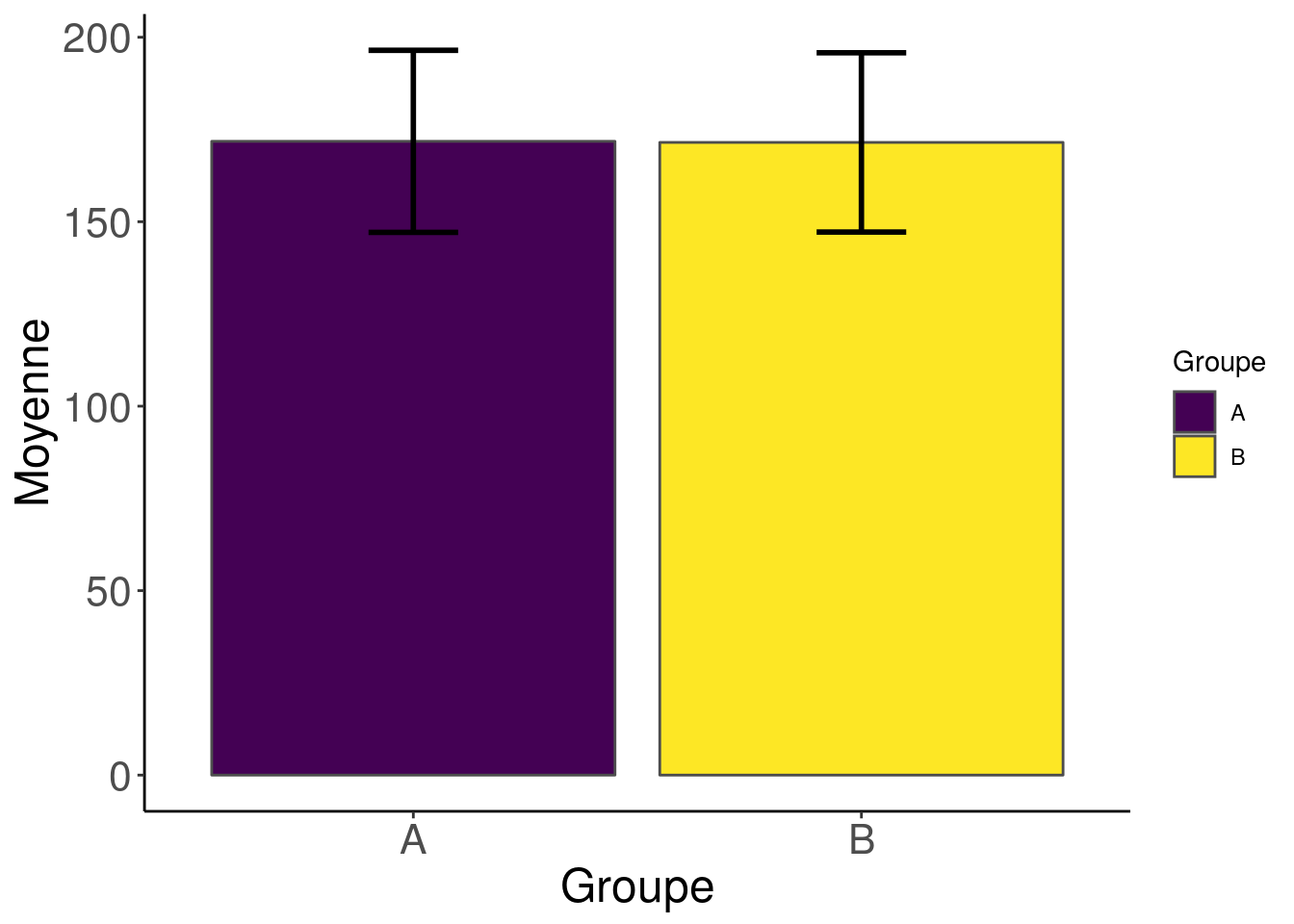

La variation a l’air plus importante dans le groupe B, mais il n’y a pas de quoi fouetter un chat, n’est-ce pas ? 😉

La boîte à moustaches

Par acquis de conscience, nous allons quand même regarder la distribution des données, on ne sait jamais. On vous a sûrement appris qu’une boîte à moustache (ou boxplot) permettait de visualiser une distribution. Alors allons-y !

Profitons-en pour enlever la double légende pour les groupes. Ça ne sert à rien d’avoir la même information à deux endroits différents. Faisons aussi passer l’axe des X au niveau du zéro de l’axe Y parce que la taille des individus ne peut être que positive et parce qu’on ne voudrait pas mentir sur l’échelle des différences…

ggplot(data, aes(x = Groupe, y = Taille, fill = Groupe)) +
  geom_boxplot(colour = "grey30") + 
  scale_fill_viridis_d() +
  scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
  guides(fill = FALSE)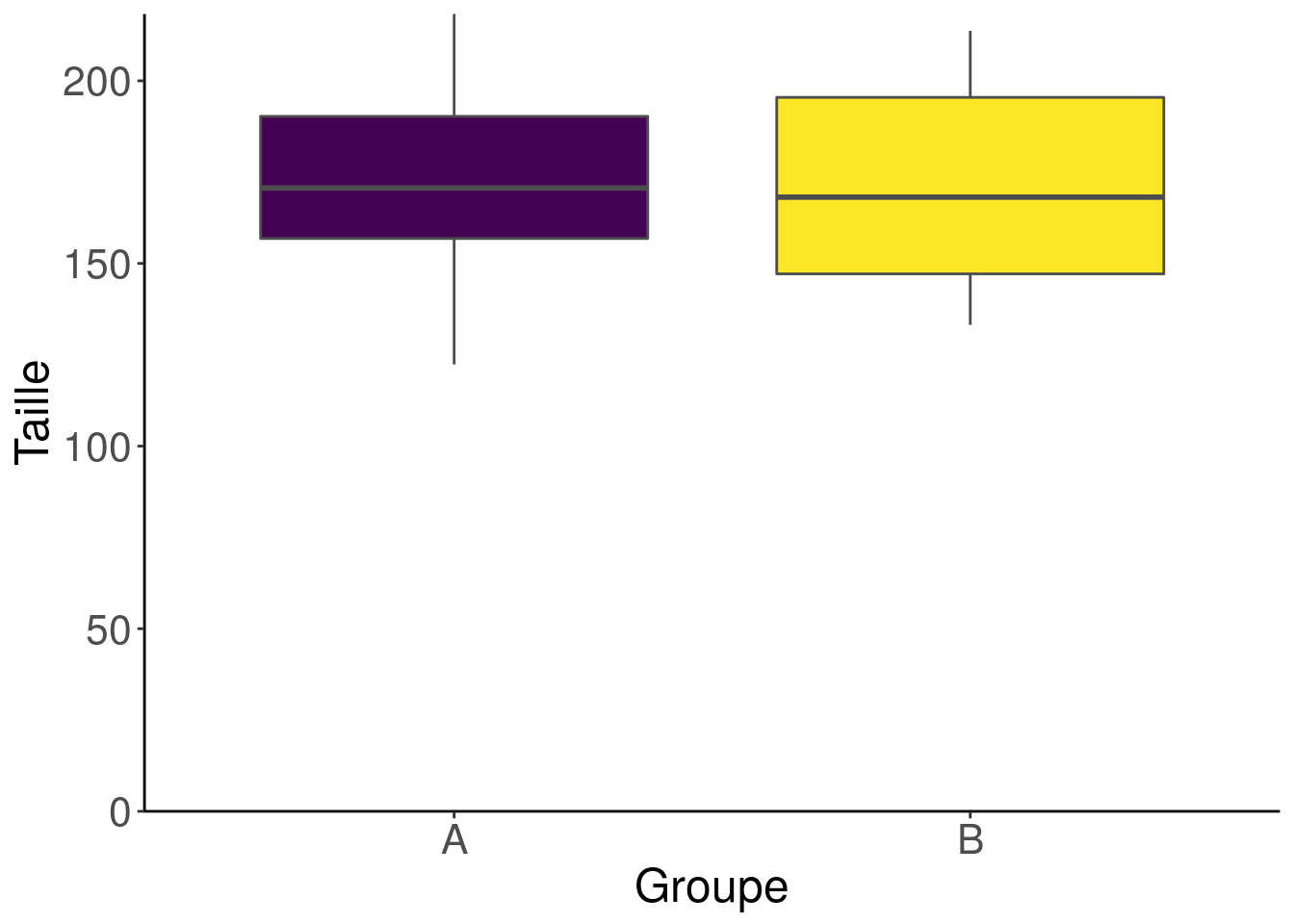

La superposition des données

En terme de comparaison de distribution, on a toujours l’impression que nos deux populations sont similaires. Et si on ajoutait les points des données ? Juste pour être vraiment sûrs !

ggplot(data, aes(x = Groupe, y = Taille, fill = Groupe)) +
  geom_boxplot(colour = "grey30") + 
  geom_jitter(width = 0.25) +
  scale_fill_viridis_d() +
  scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
  guides(fill = FALSE)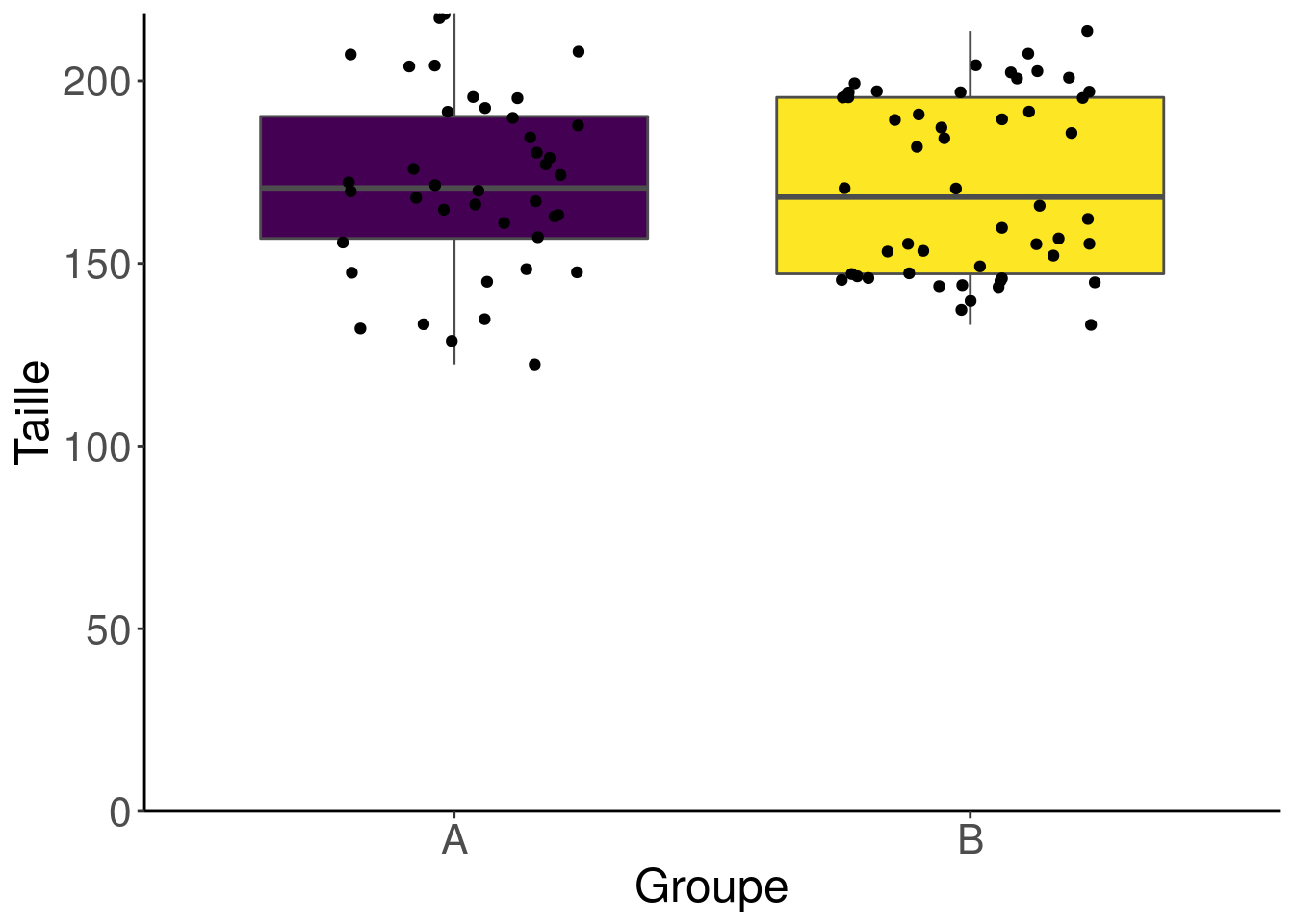

C’est marrant, avec un oeil averti, on pourrait croire qu’il y a comme deux groupes dans le groupe B, non ?

L’histogramme des données brutes

Pour le vérifier, faisons un histogramme (geom_histrogram) avec les données brutes, on verra mieux la distribution des données même si c’est peut-être moins facile à lire.

ggplot(data) + 
  geom_histogram(aes(Taille, fill = Groupe),
                 position = "identity",
                 alpha = 0.60,
                 bins = 10) +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0))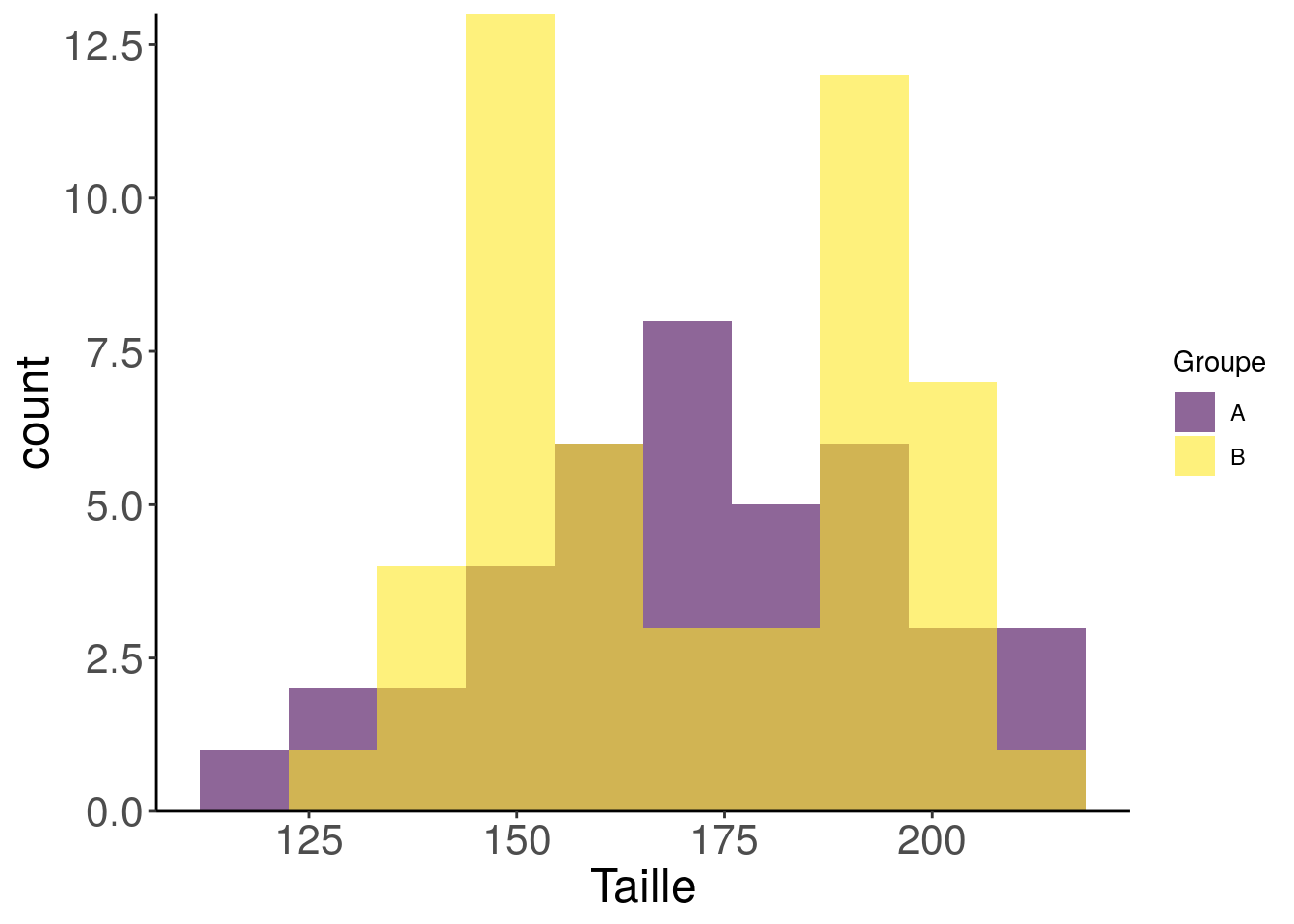

Ouppppssss ! Mais quel est ce bazar ?! Mon groupe B montre deux pics !?
Eh oui, les représentations graphiques telles que les diagrammes en barre n’utilisent que des statistiques résumées de vos données, à savoir la moyenne/médiane et l’écart-type.
Les boîtes à moustaches, montrent des statistiques supplémentaires, mais pour bien connaître la distribution des données, rien ne vaut un histogramme !

Les erreurs liées à la représentation graphique

L’erreur la plus importante est de se méprendre sur ses données. On peut voir une différence là où il n’y en a pas ou au contraire ne pas en voir alors que la différence est très importante !
N’oubliez pas qu’une représentation graphique est une simplification des données brutes. Vous pouvez perdre des informations. Il est donc important de choisir une représentation adaptée.

Un mauvais choix peut faire croire à l’absence ou à l’existence de liens entre des variables mesurées. Ne prenez pas le risque qu’un lecteur pense que vous essayez de lui mentir sur la réalité de vos données. Au passage, afficher une ‘p-valeur’, n’a jamais été un gage de votre bonne foi et ne donne pas de plus de confiance en une mauvaise représentation

En cas de doute, n’hésitez pas à retourner à la source. Regardez les données les plus brutes possibles.

La marche à suivre

Exploration des données brutes

Une première étape très importante (et généralement oubliée) est de regarder la distribution des données brutes, variable par variable.

• Utilisez un diagramme en barres (geom_bar) pour les comptages des données en catégories

ggplot(data) + 
  geom_bar(aes(Groupe, fill = Groupe), colour = "grey30") + 
  scale_fill_viridis_d() +
  scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
  guides(fill = FALSE)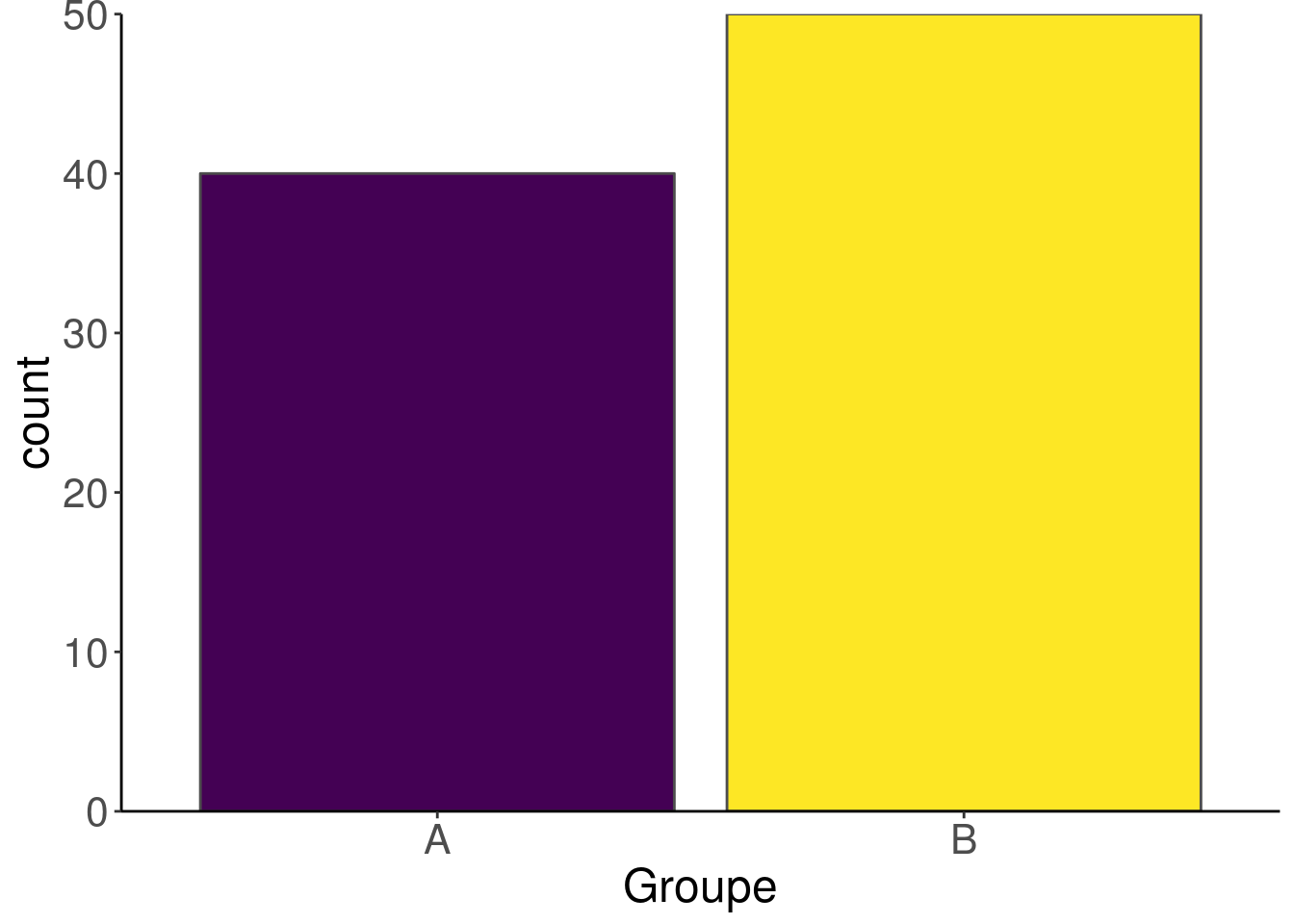

On sait ainsi que l’on n’a pas le même nombre d’individus dans les deux groupes A et B.

• Utilisez l’histogramme (geom_histogram) pour représenter les données numériques

ggplot(data) + 
  geom_histogram(aes(Taille), bins = 30)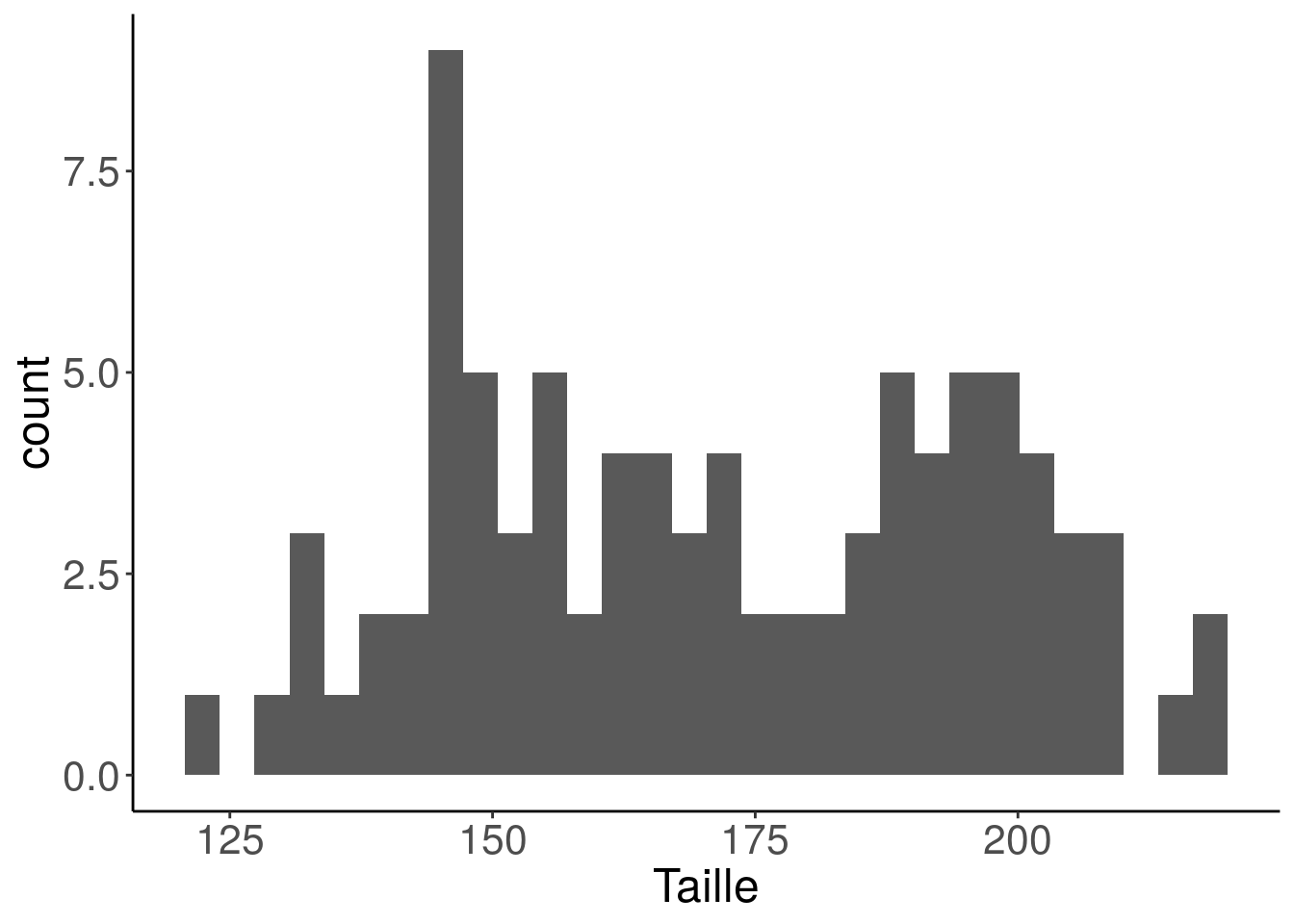

Les données de taille n’ont pas de distribution simple connue mais il semble y avoir au moins 2 groupes.

Exploration des données par croisement de variables

Une fois que l’on connaît la forme générale de chacune des variables de notre jeu de données, nous allons pouvoir regarder leur comportement en combinaison avec une ou deux autres variables. C’est à ce moment là que l’on peut réaliser l’histogramme avec les groupes séparés.

ggplot(data) + 
  geom_histogram(aes(Taille, fill = Groupe),
                 position = "identity",
                 colour = "grey30", 
                 bins = 10) +
  scale_fill_viridis_d() +
    scale_y_continuous(limits = c(0, NA),
                     expand = c(0, 0)) +
  guides(fill = FALSE) +
  facet_grid(rows = vars(Groupe))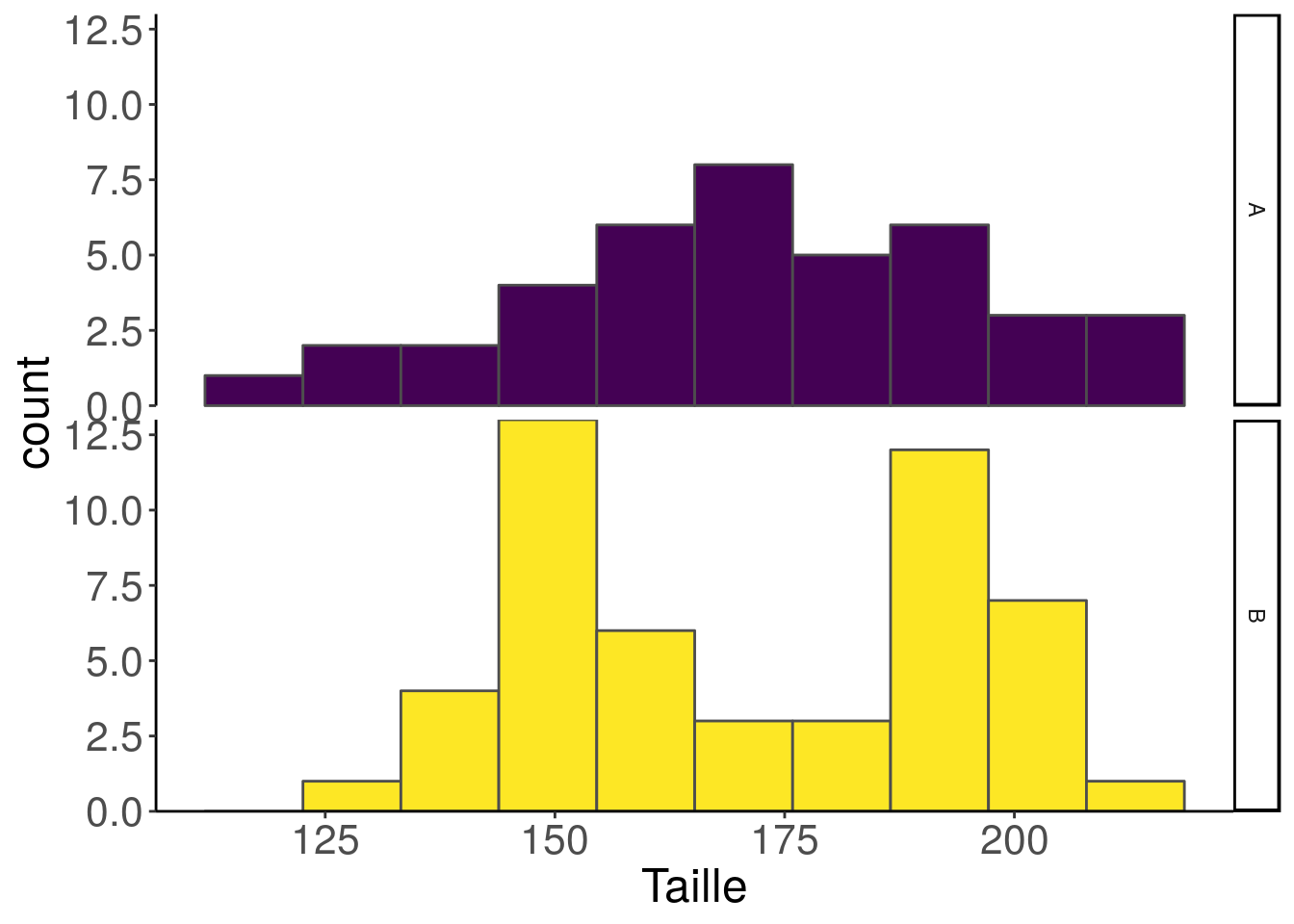

En conclusion

• Ne commencez jamais à analyser des données sans les connaître
• Regardez d’abord les variables les unes après les autres puis les relations entre elles
• Faîtes des histogrammes !
• Et pour savoir quoi choisir à la place d’un bar-bar-plot, allez voir notre article Comment se passer d’un barbarplot !

N’hésitez pas à laisser vos commentaires, questions, en bas de l’article, ils seront lus avec attention.

PS : Voici comment réaliser le jeu de données totalement factice de cet article, créé pour l’occasion !

set.seed(4321)
data <- tibble(
  Taille = c(rnorm(40, 170, 30), rnorm(25, 145, 10), rnorm(25, 195, 10)),
  Groupe = c(rep("A", 40), rep("B", 50))
)

Pour information, nous avons défini un thème par défaut pour cet article theme_set(theme_classic())