Mais où sont-elles ? Bon, il ne s’agit pas vraiment de savoir où elles ont bien pu passer, mais plutôt de comment les remplacer. Au cours de notre carrière, nous avons tous fait l’expérience de nous être cassé la tête pour savoir comment nous allions pouvoir exploiter ces données truffées de valeurs manquantes, car on le sait, la qualité de nos données est une des clés principales pour mener à bien un projet data.
La première chose à faire quand on est face à des données qui nous sont peu ou pas familières, c’est de regarder la tête qu’elles ont : un petit coup d’œil au summary et quelques graphes plus tard (voir à ce titre l’article dédié aux pièges à éviter lorsqu’on souhaite visualiser ses données : https://thinkr.fr/les-pieges-de-la-representation-de-donnees/), on a déjà une idée plus claire quant au travail de nettoyage qui nous attend.
Une autre fonction qui peut être utile pour se faire une première idée sur nos données et qui donne le nombre de valeurs manquantes par variable : skim() du package {skimr}, ou encore la fonction glimpse() du package {dplyr}:
data(iris)
# introduction de 20% de valeurs manquantes :
iris.miss <- missForest::prodNA(iris, noNA = 0.2)
# summary de base :
summary(iris.miss)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## Min. :4.400 Min. :2.200 Min. :1.000 Min. :0.100 setosa :37
## 1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300 versicolor:40
## Median :5.750 Median :3.000 Median :4.450 Median :1.300 virginica :40
## Mean :5.816 Mean :3.078 Mean :3.808 Mean :1.139 NA's :33
## 3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
## Max. :7.900 Max. :4.400 Max. :6.700 Max. :2.500
## NA's :20 NA's :32 NA's :30 NA's :35# fonction str, également un classique
str(iris.miss)## 'data.frame': 150 obs. of 5 variables:
## $ Sepal.Length: num 5.1 4.9 4.7 4.6 NA 5.4 4.6 5 4.4 4.9 ...
## $ Sepal.Width : num 3.5 3 3.2 3.1 3.6 NA 3.4 NA 2.9 3.1 ...
## $ Petal.Length: num 1.4 1.4 1.3 1.5 NA 1.7 1.4 1.5 1.4 1.5 ...
## $ Petal.Width : num 0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
## $ Species : Factor w/ 3 levels "setosa","versicolor",..: NA 1 NA 1 1 1 NA 1 1 NA ...# fonction skim, alternative à la fonction summary :
skimr::skim(iris.miss)| Name | iris.miss |
| Number of rows | 150 |
| Number of columns | 5 |
| _______________________ | |
| Column type frequency: | |
| factor | 1 |
| numeric | 4 |
| ________________________ | |
| Group variables | None |
Variable type: factor
| skim_variable | n_missing | complete_rate | ordered | n_unique | top_counts |
|---|---|---|---|---|---|
| Species | 33 | 0.78 | FALSE | 3 | ver: 40, vir: 40, set: 37 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| Sepal.Length | 20 | 0.87 | 5.82 | 0.83 | 4.4 | 5.1 | 5.75 | 6.4 | 7.9 | ▇▇▇▃▁ |
| Sepal.Width | 32 | 0.79 | 3.08 | 0.42 | 2.2 | 2.8 | 3.00 | 3.3 | 4.4 | ▃▇▆▂▁ |
| Petal.Length | 30 | 0.80 | 3.81 | 1.74 | 1.0 | 1.6 | 4.45 | 5.1 | 6.7 | ▇▁▅▇▃ |
| Petal.Width | 35 | 0.77 | 1.14 | 0.76 | 0.1 | 0.3 | 1.30 | 1.8 | 2.5 | ▇▂▆▅▃ |
# fonction glimpse
dplyr::glimpse(iris.miss)## Observations: 150
## Variables: 5
## $ Sepal.Length [3m[38;5;246m<dbl>[39m[23m 5.1, 4.9, 4.7, 4.6, NA, 5.4, 4.6, 5.0, 4.4, 4.9, 5.4, 4.8, 4.8, NA, 5.…
## $ Sepal.Width [3m[38;5;246m<dbl>[39m[23m 3.5, 3.0, 3.2, 3.1, 3.6, NA, 3.4, NA, 2.9, 3.1, 3.7, 3.4, 3.0, 3.0, 4.…
## $ Petal.Length [3m[38;5;246m<dbl>[39m[23m 1.4, 1.4, 1.3, 1.5, NA, 1.7, 1.4, 1.5, 1.4, 1.5, NA, 1.6, NA, NA, 1.2,…
## $ Petal.Width [3m[38;5;246m<dbl>[39m[23m 0.2, 0.2, 0.2, 0.2, 0.2, 0.4, 0.3, 0.2, 0.2, 0.1, 0.2, NA, NA, 0.1, 0.…
## $ Species [3m[38;5;246m<fct>[39m[23m NA, setosa, NA, setosa, setosa, setosa, NA, setosa, setosa, NA, setosa…Mais attention ! Avant de se lancer tête baissée dans l’étude des différentes méthodes d’imputation, faut-il déjà savoir identifier les données manquantes. Elles ne sont en effet pas toujours matérialisées par un clair « NA ». Il est également utile d’en comprendre les raisons.
Sommaire
Pourquoi j’ai des données manquantes ?
Parce qu’on ne vit pas encore dans le meilleur des mondes (sans blague !), de nombreux facteurs peuvent entrer en compte, selon la nature et la provenance de vos données. Les données manquantes sont rangées selon le mécanisme qui a conduit à leur absence :
– MCAR : Missing completely at random : La probabilité que la donnée soit manquante pour une variable est indépendante des autres variables, comme perdre un disque qui contient 10% des données, faire tomber un tube d’analyse sanguine, …
– MAR : Missing At Random : La probabilité que la donnée soit manquante pour une variable dépend des autres variables observé es, mais pas de la variable en question. C’est par exemple la mesure du poids qui va dépendre de l’âge (i.e. on pèse moins les adultes que les enfants).
– MNAR : Missing Not At Random : La probabilité que la donnée soit manquante pour une variable dépend de la valeur non observée. C’est l’exemple des personnes ayant des hauts revenus qui répondent moins à la question sur leur salaire, ou des patients séropositifs qui répondront moins à la question sur la séropositivité.
Données manquantes, savoir les reconnaître
« NA » est le symbole de la donnée manquante dans R, comme beaucoup d’autres langages (ne pas le confondre avec « NaN » qui signifie “not a number”, qui peut apparaître lors d’une division par zéro par exemple). Mais les données manquantes ne sont pas toujours mises à NA. Ci-dessous une liste non exhaustive de cas que nous pouvons rencontrer :
- Le cas le plus simple à identifier est le caractère vide ou l’espace pour les variables de type chaînes de caractères. Il est également possible d’avoir à faire à des « no data ».
- Dans le même type de cas de figure mais pour les variables numériques, on retrouve régulièrement les « 999 » et autres nombres volontairement incohérents.
- Les outliers constituent également des valeurs manquantes
- Dans les séries chronologiques, plusieurs cas :
- La dernière observation est répétée jusqu’à ce qu’une nouvelle donnée soit observée
- Des séquences entières sont répétées : jour/semaine/mois précédent
- 0 au lieu de NA ou parfois autre valeur constante basse
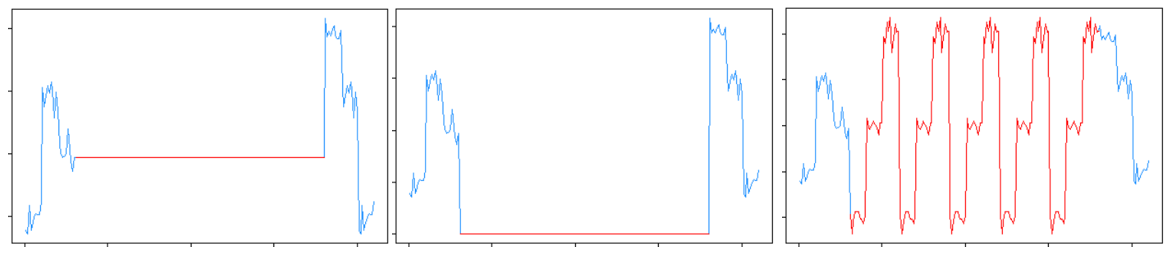
Dans un certain nombre des cas cités ci-dessus, notamment la répétition de séquences, on se trouve dans le cas où les données ont été déjà traitées par un tiers afin qu’elles ne soient pas manquantes. Les détecter peut représenter un réel enjeu car la méthode de remplacement utilisée à priori n’est peut-être pas la plus adéquate (remplacer une valeur manquante par zéro alors qu’il s’agit d’une variable dont les valeurs sont toujours comprises entre 100 et 150 ne peut pas vraiment être considéré comme une bonne idée). Nous devons garder en tête que sans données de qualité (et donc sans méthode adaptée pour la gestion des données manquantes), il sera impossible de donner du sens à nos analyses.
Visualisation des données manquantes
« Visualiser un truc qui n’existe pas… (mais t’as fumé quoi ?) » allez-vous penser… Il existe en fait nombreux packages R ont des fonctions dédiées à la représentation graphique des données manquantes – donc non ce n’est pas une idée saugrenue. L’idée est de comprendre nos données manquantes, d’en déterminer les patterns s’il y en a.
Le package {visdat}
{visdat} est un package qui permet de visualiser un jeu de données entier. La fonction vis_miss() se concentre sur les valeurs manquantes de l’ensemble de nos données : pourcentage de NA pour chaque variable et global, visualisation
library(visdat)
vis_miss(airquality)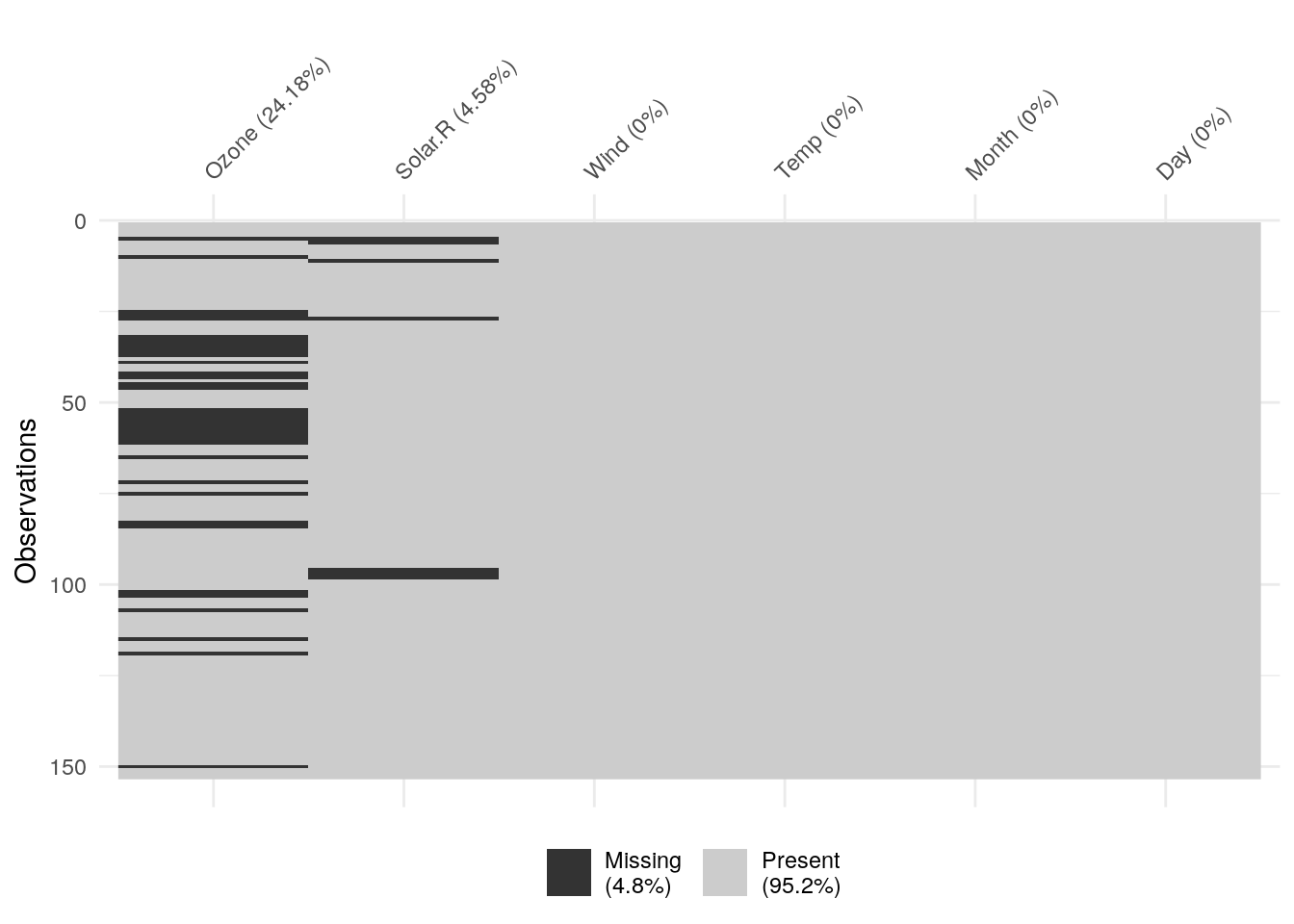
Le package {naniar}
Ce package est entièrement dédié aux données manquantes, avec en particulier 4 fonctions permettant de les visualiser, non seulement variable par variable, mais également les relations entre elles.
- la fonction
geom_miss_points()remplace les NA par des valeurs 10% plus basses que la valeur minimum observée de la variable, ce qui permet de les visualiser comme ci-dessous :
library(naniar)
ggplot(data = airquality) +
aes(x = Ozone, y = Solar.R) +
geom_miss_point()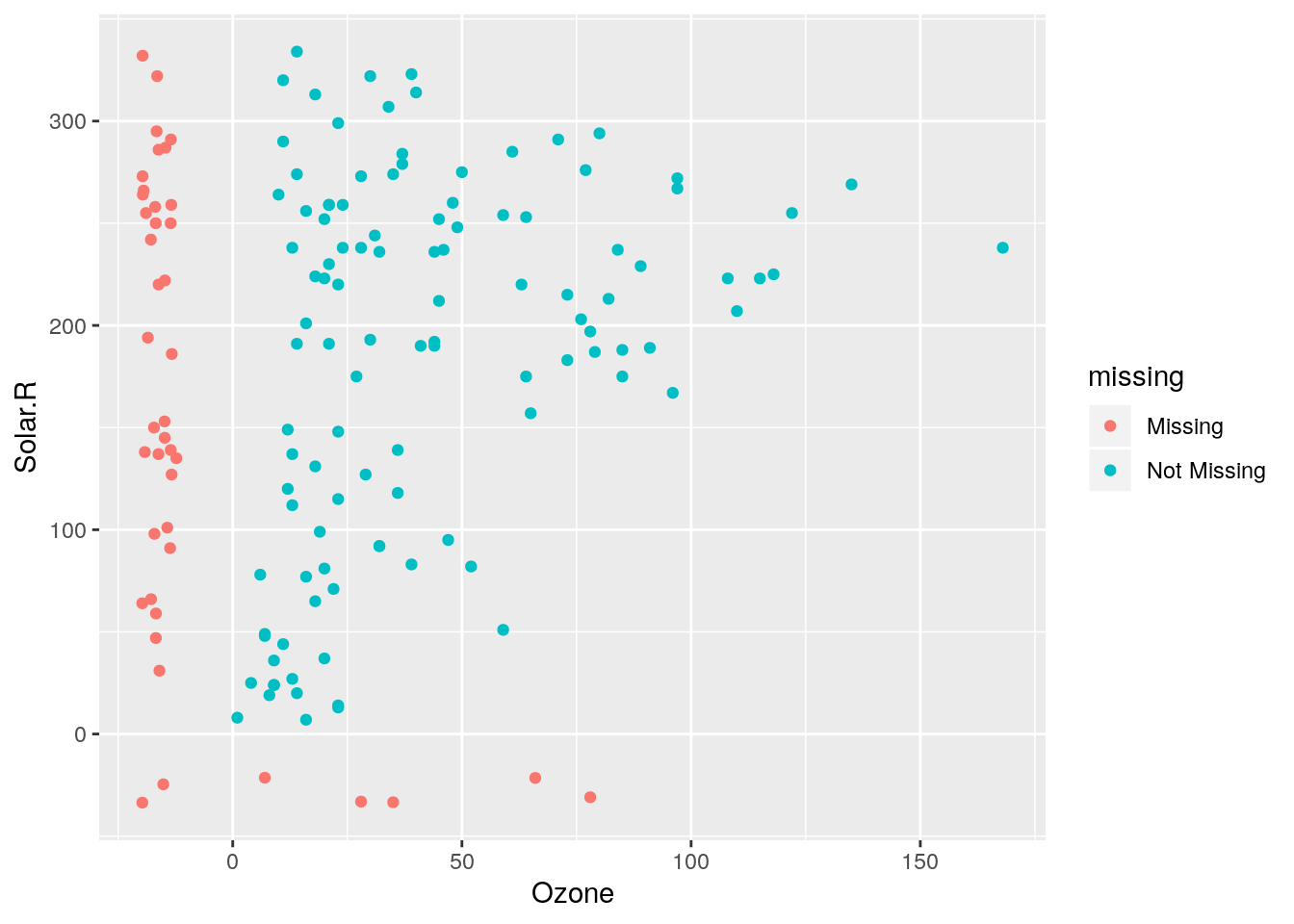
- La fontion
gg_miss_var()présente une autre approche pour la visualisation des données manquantes :
gg_miss_var(airquality)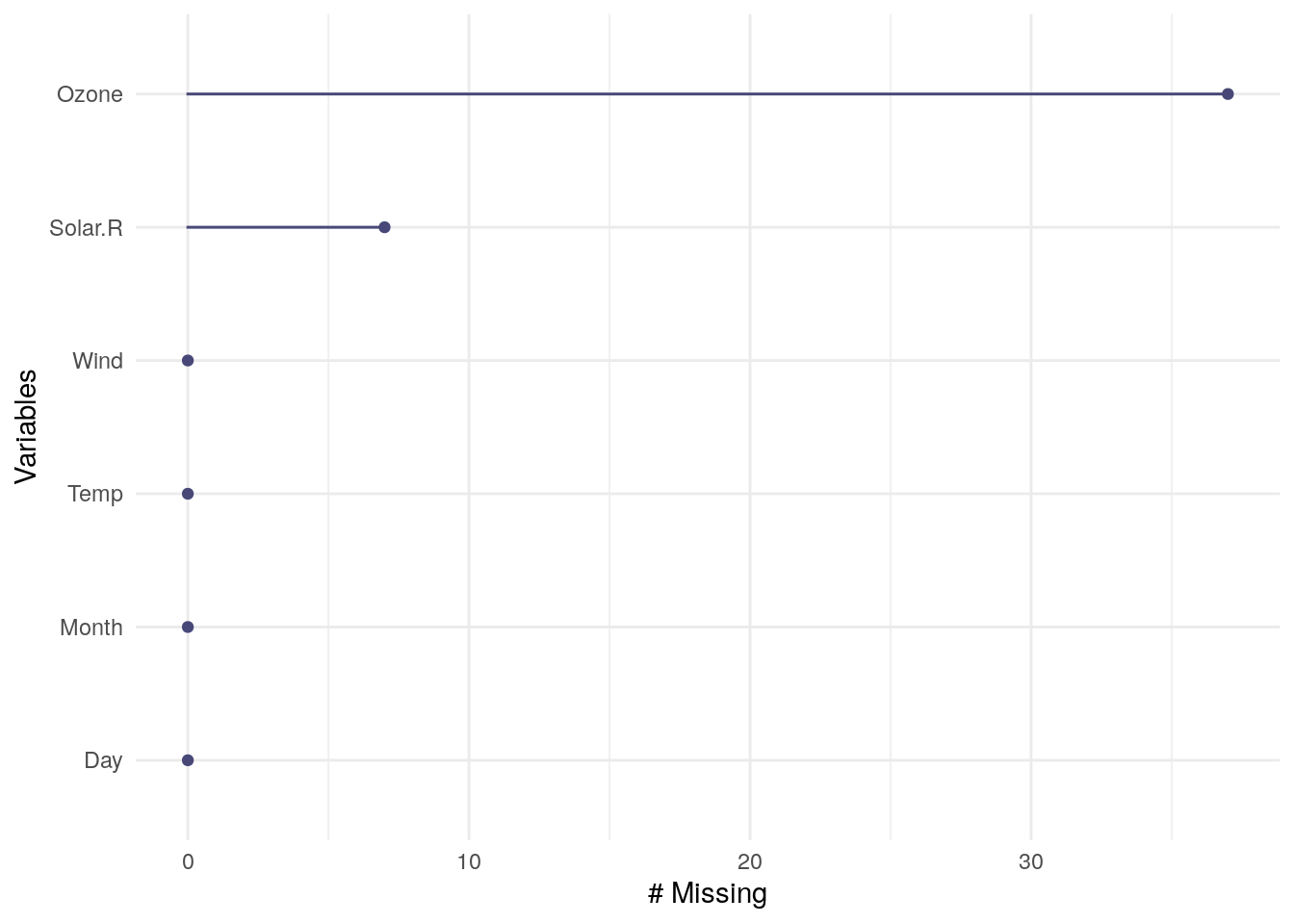
- La fonction
gg_miss_case():
gg_miss_case(airquality)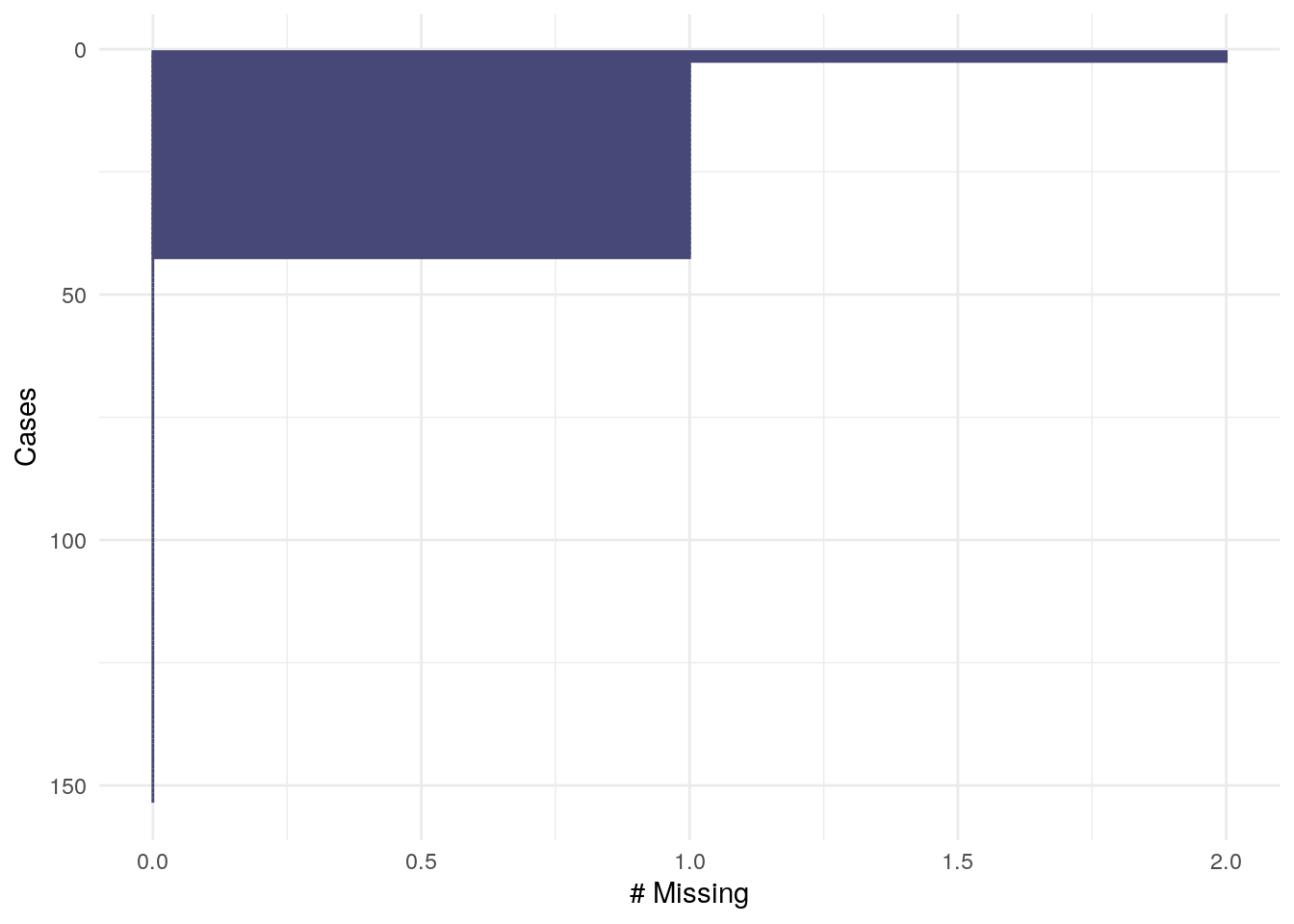
- La fonction
gg_miss_fct()plot le nombre de valeurs manquantes de chaque colonne en fonction d’une variable catégorielle du jeu de données :
gg_miss_fct(x = riskfactors, fct = marital)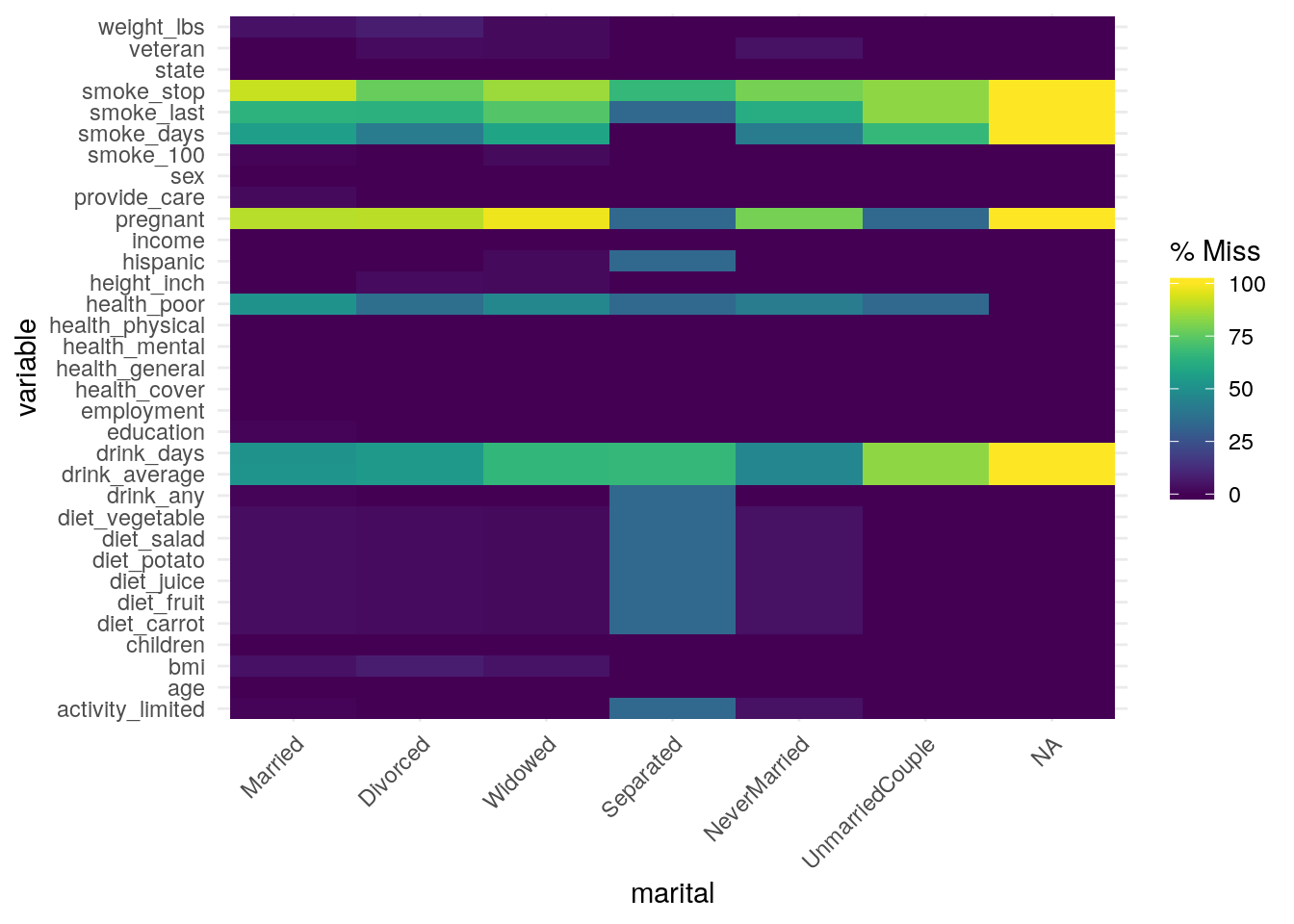
Le package {UpSetR}
La fonction gg_miss_upset() peut être utile pour visualiser les combinaisons de NA les et intersections de variables.
library(UpSetR)
gg_miss_upset(riskfactors)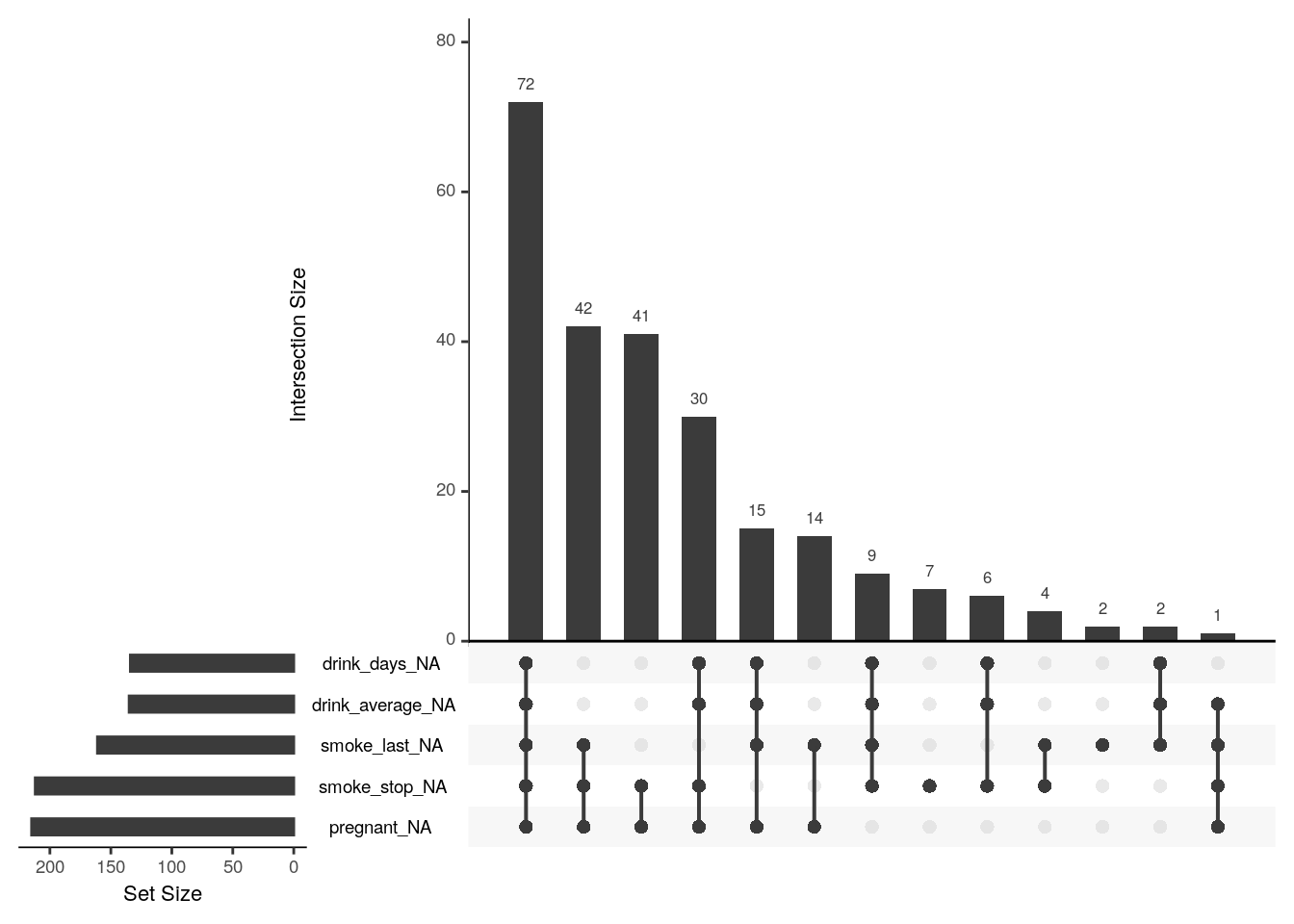
Les différentes stratégies d’imputation
Impu… quoi ? L’imputation des données manquantes est simplement le fait de remplacer ces valeurs, avec la méthode la plus adéquate.
Si la quantité de données manquantes peut être considérée comme négligeable, au regard de la taille de notre échantillon, il est possible d’envisager de simplement supprimer les observations concernées, et ainsi de ne pas introduire de biais dans notre analyse. L’option R correspondant à cette décisision est de mettre le paramètre na.rm à TRUE, mais ce n’est pas l’option par défaut, en effet cela suppose une perte d’information, et nous ne sommes pas toujours prêts à faire ce sacrifice.
Bon, et sinon, on fait quoi ?
La méthodologie que nous mettons en place pour remplacer nos fameuses données manquantes est très étroitement liées à notre jeu de données ; beaucoup de techniques s’appuient en effet sur les autres variables que nous avons à notre disposition, quelques-uns des exemples ci-dessous illustrent ce propos.
Dans certains cas, des méthodes très simples peuvent être mises en œuvre. Quelques exemples :
- Pour les variables catégorielles :
- Remplacement par la valeur dominante (ie la plus fréquente)
- Remplacement par la valeur dominante par classe (si on considère par exemple la taille d’une personne, mise sous forme catégorielle : la valeur dominante sera différente selon le sexe)
- Réfléchir au sens de la donnée manquante : n’y a-t-il pas de sens à cette absence de donnée ? Cela mérite peut-être la création d’une nouvelle catégorie
- Pour les variables numériques, le package
{zoo}offre de nombreuses solutions :- Remplacement par la moyenne globale ou la moyenne par classe :
na.aggregate. C’est la méthode la plus populaire, mais elle ne constitue que rarement une solution viable. Voyons un exemple simple :
- Remplacement par la moyenne globale ou la moyenne par classe :
# Génération d'un jeu de données bivarié, distribution normale
df_bivar <- data.frame(x = rnorm(50, 0, 1), y = rnorm(50, 10, 10))
# Introduction artificielle de données manquantes (20%) :
df_miss <- df_bivar
df_miss$y[sample(1:nrow(df_miss), size = 10)] <- NA
df_miss$any_na <- ifelse(is.na(df_miss$y), "donnée imputée", "donnée originale")
# Imputation des données manquantes par la moyenne
library(zoo)
df_miss$y <- na.aggregate(df_miss$y, FUN = mean)# Visualisation
plot_ly(data = df_miss, x = ~x, y = ~y, color = ~any_na, colors = "Set2") -
- Répétition de la dernière ou de la prochaine valeur observée :
na.locf()
- Répétition de la dernière ou de la prochaine valeur observée :
library(zoo)
bz <- zoo(c(2, NA, 1, 4, 5, 2))
# répétition de la dernière valeur observée
na.locf(bz)## 1 2 3 4 5 6
## 2 2 1 4 5 2# répétition de la prochaine valeur observée
na.locf(bz, fromLast = TRUE)## 1 2 3 4 5 6
## 2 1 1 4 5 2-
- Interpolation entre points : pour les variables triées en fonction du temps ou en fonction d’une autre variable. Interpolation linéaire grâce à la fonction
na.approx(), interpolation spline cubique avec la fonctionna.spline(). Attention, ici on suppose que chaque observation est distante d’une unité, et non indexée par la variable de tri.
- Interpolation entre points : pour les variables triées en fonction du temps ou en fonction d’une autre variable. Interpolation linéaire grâce à la fonction
library(zoo)
library(plotly)
# simualtion des données
z <- c(rnorm(10, 10), rep(NA, 5), rnorm(10, 10))
# interpolation linéaire
z_lin <- na.approx(z)
# interpolation spline
z_spline <- na.spline(z)
data_z <- data.frame(x = 1:25, z = z, z_lin = z_lin, z_spline = z_spline)
# plot
p <- plot_ly(data_z, x = ~x) %>%
add_trace(y = ~z_lin, name = "linéaire", type = "scatter", mode = "lines") %>%
add_trace(y = ~z_spline, name = "spline", type = "scatter", mode = "lines") %>%
add_trace(y = ~z, name = "z", type = "scatter", mode = "lines+markers") %>%
layout(
title = "Interpolation entre points",
xaxis = list(title = ""),
yaxis = list(title = "")
)p-
- Interpolation grâce à la méthode des kNN : l’idée est de calculer les distances entre observations, et d’attribuer aux valeurs manquante la moyenne des valeurs observées chez les k plus proches voisins : fonction
kNN()du package{VIM}.
- Interpolation grâce à la méthode des kNN : l’idée est de calculer les distances entre observations, et d’attribuer aux valeurs manquante la moyenne des valeurs observées chez les k plus proches voisins : fonction
library(VIM)
# données avec valeurs manquantes :
data(sleep)
# imputation grâce à la méthode des kNN :
kNN(sleep)- Pour les séries temporelles :
- On l’a vu précédemment, la répétition d’une séquence peut constituer une solution viable
- La fonction
na.StructTS()du package{zoo}permet de reproduire la saisonnalité de la série en utilisant le filtre saisonnier de Kalman
z <- zooreg(
rep(10 * seq(8), each = 4) + rep(c(3, 1, 2, 4), times = 8),
start = as.yearqtr(2000), freq = 4
)
z[25] <- NA
zout <- na.StructTS(z)
data_z <- data.frame(z = z, z_out = zout)
# plot
p <- plot_ly(data_z) %>%
add_trace(y = ~zout, name = "Kalman", type = "scatter", mode = "lines") %>%
add_trace(y = ~z, name = "avec NA", type = "scatter", mode = "lines") %>%
layout(
title = "na.StructTS",
xaxis = list(title = ""),
yaxis = list(title = "")
)pC’est bien beau, mais c’est pas un peu du bricolage tout ça ?
Si ces méthodes peuvent être satisfaisantes dans certains cas, elles ne sont pas assez solides dans d’autres, c’est pourquoi il existe des algorithmes d’imputation bien plus sophistiqués, et on est chanceux, la formidable communauté R s’est déjà penchée sur le sujet et nous offre des packages très bien faits.
Le package {bcv}
La fonction impute.svd() du package {bcv} permet d’appliquer l’algorithme de la décomposition en valeurs singulières afin de prédire les valeurs manquantes.
library(bcv)
# Génération d'une matrice avec données manquantes
u <- rnorm(20)
v <- rnorm(10)
xfull <- u %*% rbind(v) + rnorm(200)
miss <- sample(1:20, 5)
x <- xfull
x[miss] <- NA
# imputation des données manquantes avec une approximation SVD de rang 1
xhat <- impute.svd(x, 1)$x
data_z <- data.frame(x = 1:20, y_miss = x[, 1], y = xhat[, 1])
# plot
p <- plot_ly(data_z, x = ~x) %>%
add_trace(y = ~y, name = "après imputation", type = "scatter", mode = "lines") %>%
add_trace(y = ~y_miss, name = "avec NA", type = "scatter", mode = "lines") %>%
layout(
title = "Imputation SVD",
xaxis = list(title = ""),
yaxis = list(title = "")
)pLe package {mice} (Multivariate Imputation via Chained Equations)
C’est l’une des stars des packages d’imputation de données manquantes. Son utilisation suppose que les données soient MAR (Missing At Random). A chaque variable est associé un modèle d’imputation, conditionnellement aux autres variables du jeu de données : si on a Xk variables, les données manquantes de la variable Xi seront remplacées par les prédictions d’un modèle créé à partir des autres variables. Ce package présente une solution très complète au vu du nombre de méthodes implémentées, je vous invite à consulter l’aide du package pour en avoir la liste exhaustive. Pour n’en citer que quelques-unes, le paramètre method de la fonction mice() peut prendre les valeurs suivantes :
- Pour tout type de variable :
pmm: predictive mean matchingcart: arbres de régression et classificationrf: modèle random forest
- Pour les variables numériques :
norm: régression linéairequadratic
- Pour les variables binaires :
logreg: régression logistique
- Pour les variables factorielles :
polyreg: régression logistique multiplelda: analyse discriminante linéaire
- Pour les variables factorielles ordonnées :
polr: modèle de probabilité proportionnelle (proportional odds model)
Une autre raison pour laquelle ce package est encensé par la communauté est qu’il présente de nombreuses fonctions permettant de faire un tas de choses, en plus de l’imputation, comme :
- Visualiser les données manquantes
- Diagnostiquer la qualité des valeurs imputées
- Analyser chaque ensemble de données complétées
- Incorporer des méthodes d’imputation personnalisées
Ci-dessous un exemple d’utilisation de ce package :
library(mice)
# données avec NA :
data_mice <- nhanes2
summary(data_mice)## age bmi hyp chl
## 20-39:12 Min. :20.40 no :13 Min. :113.0
## 40-59: 7 1st Qu.:22.65 yes : 4 1st Qu.:185.0
## 60-99: 6 Median :26.75 NA's: 8 Median :187.0
## Mean :26.56 Mean :191.4
## 3rd Qu.:28.93 3rd Qu.:212.0
## Max. :35.30 Max. :284.0
## NA's :9 NA's :10# Visualisation des données manquantes :
md.pattern(data_mice)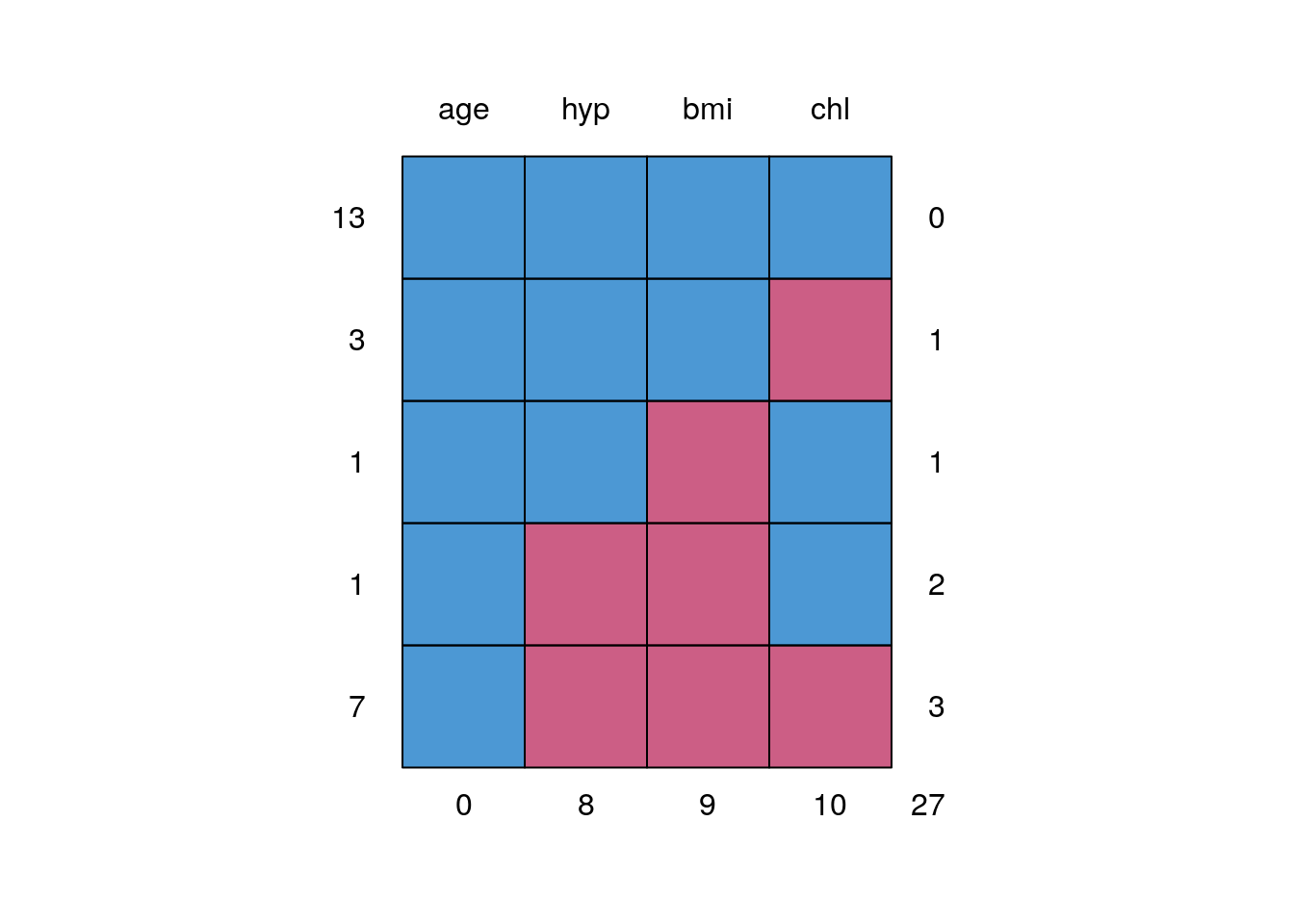
## age hyp bmi chl
## 13 1 1 1 1 0
## 3 1 1 1 0 1
## 1 1 1 0 1 1
## 1 1 0 0 1 2
## 7 1 0 0 0 3
## 0 8 9 10 27Cette visualisation nous permet de déterminer rapidement où sont les valeurs manquantes de notre jeu de données. Ici on voit :
- 13 observations n’ont aucune valeur manquante
- pour 3 observations la valeur de chl est manquante
- pour 1 observation, la valeur de bmi est manquante
- etc…
# Imputation multiple (5) sur données mixtes, avec une méthode différente sur chaque colonne :
imputed <- mice(data_mice, meth = c("sample", "pmm", "logreg", "norm"), m = 5, printFlag = FALSE)
# voir les valeurs imputées :
# 5 imputations par variable
imputed$imp$bmi## 1 2 3 4 5
## 1 29.6 22.5 22.5 25.5 33.2
## 3 26.3 28.7 29.6 33.2 29.6
## 4 33.2 26.3 21.7 29.6 27.4
## 6 22.7 21.7 22.5 29.6 24.9
## 10 33.2 35.3 21.7 22.7 22.5
## 11 27.2 27.2 29.6 35.3 25.5
## 12 27.4 27.2 22.0 22.5 27.4
## 16 28.7 29.6 35.3 22.0 27.5
## 21 28.7 27.2 28.7 33.2 35.3Le paramètre m représentant le nombre d’imputation effectuées. La fonction complete() permet de sélectionner une des imputations afin de compléter notre jeu de données :
# données complétées avec la 2nde imputation :
imputed_data <- mice::complete(imputed, 2)La fonction with() permet de construire des modèles sur chaque jeu de données générés :
fit <- with(data = imputed, exp = lm(bmi ~ hyp + chl))La fonction pool() permet comme son nom l’indique de combiner les modèles :
combined <- mice::pool(fit)Le package {Amelia}
Du nom de la première femme aviateur a avoir traversé l’Atlantique en solitaire (Amelia Earhart), supposément disparue lors d’un survol de l’océan Pacifique (elle est « missing », comme nos missing data : je n’arrive pas à savoir si je trouve ça cool ou de mauvais goût de l’avoir nommé ainsi), ce package, tout comme le package {mice} précédemment décrit, permet de réaliser des imputations multiples, ce qui a pour avantage de réduire le biais tout en augmentant la pertinence de l’imputation. Autre point commun, les données manquantes sont supposées MAR, mais ici s’ajoute la condition que les variables du jeu de données doivent avoir une distribution normale multivariée, ce qui implique une transformation des variables à priori, et donc plus de travail que si l’on utilise le package {mice} qui prend en charge tout type de données.
La fonction amelia() présente un algorithme qui combine l’algorithme classique du maximum de vraisemblance avec une approche boostrap, ce qui en fait une méthode rapide et robuste.
library(Amelia)
data(africa)
summary(africa)## year country gdp_pc infl trade
## Min. :1972 Burkina Faso:20 Min. : 376.0 Min. : -8.400 Min. : 24.35
## 1st Qu.:1977 Burundi :20 1st Qu.: 513.8 1st Qu.: 4.760 1st Qu.: 38.52
## Median :1982 Cameroon :20 Median :1035.5 Median : 8.725 Median : 59.59
## Mean :1982 Congo :20 Mean :1058.4 Mean : 12.753 Mean : 62.60
## 3rd Qu.:1986 Senegal :20 3rd Qu.:1244.8 3rd Qu.: 13.560 3rd Qu.: 81.16
## Max. :1991 Zambia :20 Max. :2723.0 Max. :127.890 Max. :134.11
## NA's :2 NA's :5
## civlib population
## Min. :0.0000 Min. : 1332490
## 1st Qu.:0.1667 1st Qu.: 4332190
## Median :0.1667 Median : 5853565
## Mean :0.2889 Mean : 5765594
## 3rd Qu.:0.3333 3rd Qu.: 7355000
## Max. :0.6667 Max. :11825390
## a.out <- amelia(x = africa, cs = "country", ts = "year", logs = "gdp_pc")## -- Imputation 1 --
##
## 1 2
##
## -- Imputation 2 --
##
## 1 2 3
##
## -- Imputation 3 --
##
## 1 2 3
##
## -- Imputation 4 --
##
## 1 2 3
##
## -- Imputation 5 --
##
## 1 2 3summary(a.out)##
## Amelia output with 5 imputed datasets.
## Return code: 1
## Message: Normal EM convergence.
##
## Chain Lengths:
## --------------
## Imputation 1: 2
## Imputation 2: 3
## Imputation 3: 3
## Imputation 4: 3
## Imputation 5: 3
##
## Rows after Listwise Deletion: 115
## Rows after Imputation: 120
## Patterns of missingness in the data: 3
##
## Fraction Missing for original variables:
## -----------------------------------------
##
## Fraction Missing
## year 0.00000000
## country 0.00000000
## gdp_pc 0.01666667
## infl 0.00000000
## trade 0.04166667
## civlib 0.00000000
## population 0.00000000plot(a.out)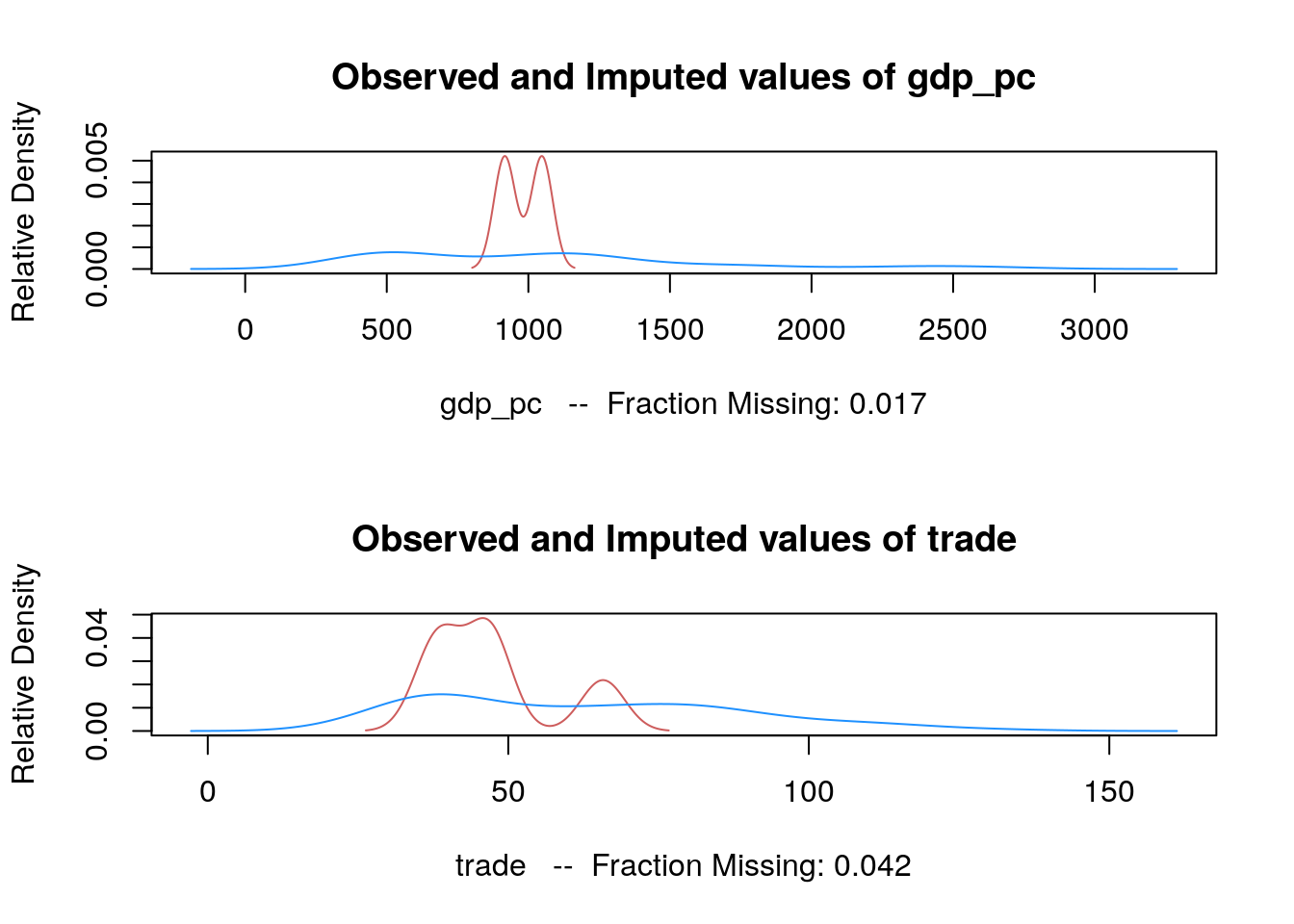
# Accéder aux différentes imputations :
# a.out$imputations[[2]]Le package {missForest}
Comme son nom l’indique, ce package propose d’utiliser une méthode de complétion basée sur les forêts aléatoires. Rapidement : pour chaque variable est construit un modèle random forest dont les prédictions permettront de remplacer les valeurs manquantes. L’option permettant de retourner l’erreur out of bag liée à chaque variable permet un haut niveau de contrôle pour les imputations au niveau de chaque variable.
library(missForest)
data(iris)
# Introduction artificielle de données manquantes (20%) :
iris.miss <- prodNA(iris, noNA = 0.2)
# Imputation des données manquantes :
iris.imputed <- missForest(iris.miss, xtrue = iris)## missForest iteration 1 in progress...done!
## missForest iteration 2 in progress...done!
## missForest iteration 3 in progress...done!
## missForest iteration 4 in progress...done!# erreur out of bag :
iris.imputed$OOBerror## NRMSE PFC
## 0.142087759 0.008928571# erreur d'imputation si disponible (si on a fourni xtrue) :
iris.imputed$error## NRMSE PFC
## 0.2246874 0.1052632# données imputées :
# iris.imputed$ximpLe package {Hmisc}
Connu pour plein d’autres raisons que l’imputation, ce package a aussi sa place dans cet article grâce à ses fonctions impute() (qui remplace les valeurs manquantes d’une variable par sa moyenne, valeur maximale ou minimale) et aregImpute() qui permet l’imputation par moyenne utilisant des méthodes de models additifs de régression, bootstrapping et de PMM (Predictive Mean Matching).
library(Hmisc)
data(iris)
# Introduction artificielle de données manquantes (20%) :
iris.miss <- prodNA(iris, noNA = 0.2)
# imputation avec la moyenne:
iris.miss$imputed_mean <- with(iris.miss, impute(Sepal.Length, mean))
# avec argeImpute :
areg_impute <- aregImpute(~ Sepal.Length + Sepal.Width + Petal.Length + Petal.Width + Species, data = iris.miss, n.impute = 5)## Iteration 1
Iteration 2
Iteration 3
Iteration 4
Iteration 5
Iteration 6
Iteration 7
Iteration 8 # données imputées :
# areg_impute$imputedLe package {mi}
MI, vous vous en doutez, est pour Multiple Imputation. Comme certains packages ci-dessus, celui-ci propose des modèles d’imputation multiple couplés à la méthode PMM, mais il présente quelques avantages supplémentaires comme par exemple les fonctions hist() et Rhats() permettent un diagnostic graphique des modèles d’imputation et de la convergence des processus d’imputation.
library(mi)
data(iris)
# Introduction artificielle de données manquantes (20%) :
iris.miss <- prodNA(iris, noNA = 0.2)
# imputation :
mi_impute <- mi(iris.miss)
# summary(mi_impute)Pour conclure :
Comme le souligne Yves Gallien dans le commentaire ci-dessous, les algorithmes d’imputations peuvent être très efficaces, tout dépend du mécanisme qui a conduit à la présence de données manquantes et de la disponibilité des autres données qui peuvent ou non aider à retrouver les données manquantes. Si vous avez beaucoup de données manquantes mais peu de variables, il n’y aura toutefois pas de solution magique…





Laisser un commentaire