Vous connaissez l’expression : jamais deux sans trois ! Suite de notre série sur le machine learning avec R.
Sommaire
Machine learning 103 : k-mean clustering
Avant de nous lancer dans le clustering avec R, commençons par un petit tour du côté de la langue de Molière : en français, le clustering est appelé « partionnement de données ». En quoi ça nous avance ? Eh bien, nous allons d’abord faire un tour dans notre livre de maths de chevet, histoire de nous rafraichir la mémoire en nous rappelant que « une partition de l’ensemble E est une famille de parties non vides de E, disjointes deux à deux, et dont la réunion est égale à E ».
Autrement dit, lorsque l’on partitionne un ensemble E, on le sépare en plusieurs parties selon une règle définie, de façon à ce que la somme des partie constituent E. Par exemple, nous pouvons partitionner l’ensemble des travailleurs d’une entreprise en fonction de leur poste.
Le clustering, comment ça marche ?
Le clustering est une méthode de classification non supervisée. Autrement dit, les classes des partitions ne sont pas prédéfinies, c’est-à-dire non inclues dans le jeu de données d’origine. Théoriquement, il existe un grand nombre de clusterings possibles : un dataset de 10.000 individus peut-être divisé en 10.000 clusters de 1, ou en un cluster de 10.000 (mais bon, ça ne serait que peu utile, non ?).
Que cherche à faire le modèle de clustering ? Ce dernier va définir un critère de similitude entre vos individus, basé sur des variables. Ensuite, ce calcul va créer un nombre k de classes au sein desquelles les individus sont le plus semblables possible, tout en maximisant la dissimilitude entre les classes. On cherche ainsi à rendre les classes les plus compacts possible, tout en étant les plus séparées possible. Enfin, une fois ce modèle défini, tout nouvel entrant se verra assigner une nouvelle classe.
Comment se construit un modèle de clustering ? Eh bien, nous devrions plutôt dire « les » modèles, car nous pouvons utiliser beaucoup de méthodes différentes. Ici, nous n’allons en évoquer qu’une : la méthode des « k-mean ».
Les k-means
Alors, comment marche un clustering en k-means ? D’abord, vous devez paramétrer un nombre de centres de cluster (admettons 5), qui sont placés de manière aléatoire. Ensuite, chaque point de votre jeu de données est assigné au centre dont il est le plus proche. Chaque cluster reçoit un nouveau centroïde, selon une mesure de centralité (dans notre cas une moyenne de distance), et chaque point est assigné au centroïde dont il est le plus proche. Ce processus est répété jusqu’à ce que la compacité et la séparation soit maximales.
Pourquoi répéter le processus ? Un algorithme de k-mean dispose d’une composante aléatoire, nécessitant de répéter l’assignation plusieurs fois avant de trouver le meilleur modèle. Justement, c’est quoi le meilleur modèle ? Dans R, l’algorithme considère que le modèle est le meilleur quand il a défini un « total within cluster sum of squares » minimum. Ne froncez pas les sourcils, cette mesure est au final assez aisée à saisir : l’algorithme fait une première boucle, en assignant un centroïde aléatoire. Puis, il calcule la distance de chaque point avec le centre de son cluster : une distance mise au carré. Toutes ces distances sont calculées pour chaque point à l’intérieur de chaque cluster. L’objectif étant d’arriver à un modèle où la somme de la distance entre chaque point et son cluster est minimale, et la distance entre les clusters maximale… autrement dit, un modèle compact et séparé !
k-means et dimensions
Avant de vous lancer dans les k-means, gardez bien en tête leur forte sensibilité au grand nombre de variables — c’est le fameux « curse of dimensionality » de nos amis anglo-saxons, que nous avons traduit par « fléau de la dimension ». De quoi s’agit-il ? En clair, vous vous souvenez qu’un algorithme de clustering définit une distance entre les observations, avant de les grouper en fonction de ces distances.
Et bien, plus le nombre de variables (et donc les dimensions de l’espace dans lequel on cherche à rapprocher des voisins) augmente, plus les données deviennent éparses, et potentiellement isolées. Un phénomène qui rend caduc la notion de « voisin » — et le classement en clusters moins efficace. Dans certains cas, le « voisin » le plus proche est peut-être si éloigné qu’il n’a plus rien en commun avec celui dont on essaye de le rapprocher.
Avec R
Bon, passons maintenant à la pratique avec R (c’est pour ça qu’on est là, non ?). La fonction pour réaliser des k-means avec R est… roulement de tambour… kmeans() !
Pour exemplifier le partitionnement de données avec R, nous allons nous baser sur un dataset disponible sur Kaggle : Men’s Professional Basketball, compilant les données de joueurs de basket de la ligue américaine. Commençons tout simplement par le charger, puis conserver les colonnes numériques.
library(tidyverse)
dataset <- read_csv("basketball_player_allstar.csv")
support <- dataset %>%
select(minutes, points, rebounds, assists, fg_attempted, fg_made, ft_attempted, ft_made) %>%
na.omit()
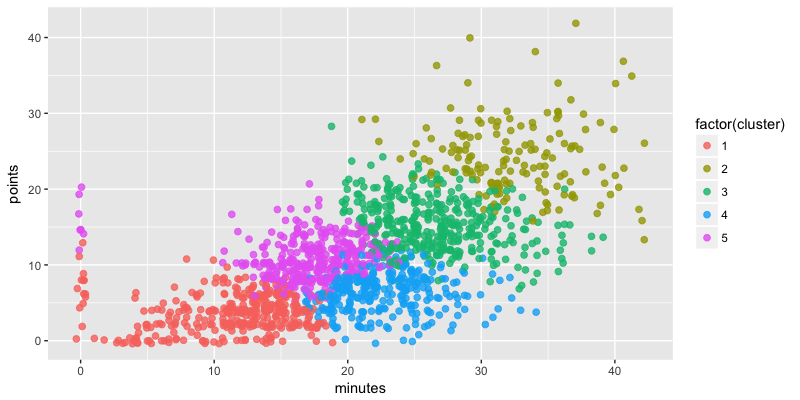
Ensuite, direction la fonction de k-mean. Cette dernière prend trois arguments principaux : votre matrice de données, le nombre de clusters, et le nombre d’itérations de votre algorithme. Essayons d’abord avec 5 clusters, et un volume de 20 itérations.
set.seed(2811)
km_model <- support %>%
kmeans(centers = 5, nstart=20)
support$cluster <- km_model$cluster
ggplot(support, aes(minutes, points, col = factor(cluster))) +
geom_point(size = 2, alpha = 0.8, position = "jitter")
Bien. Mais voilà, nous avons choisi 5 clusters, sans véritables raisons. Alors, comment peut-on choisir le meilleur volume ? Pour cela, nous allons créer un scree plot, qui compile le ratio entre le total within cluster sum of squares et le total sum of square. Il s'agit ici de repérer visuellement le "coude" du graphique, qui se situera au nombre idéal de clusters. À cet emplacement, l'ajout d'un cluster supplémentaire n'apportera pas une diminution de ratio assez intéressante pour compenser la perte d'information apportée par un cluster supplémentaire.
ratio_ss <- data.frame(cluster = seq(from = 1, to = 9, by = 1))
for (k in 1:9) {
km_model <- kmeans(support, k, nstart = 20)
ratio_ss$ratio[k] <- km_model$tot.withinss / km_model$totss
}
ggplot(ratio_ss, aes(cluster, ratio)) +
geom_line() +
geom_point()
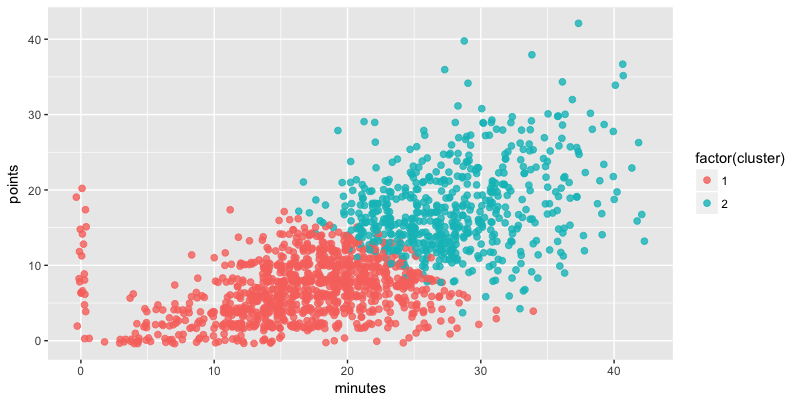
Nous voyons donc que le nombre de clusters idéal pour notre jeu de données se situe entre 2 et 3. Affichons ces deux mesures :
km_model <- support %>%
kmeans(centers = 2, nstart=20)
support$cluster <- km_model$cluster
ggplot(support, aes(minutes, points, col = factor(cluster))) +
geom_point(size = 2, alpha = 0.8, position = "jitter")
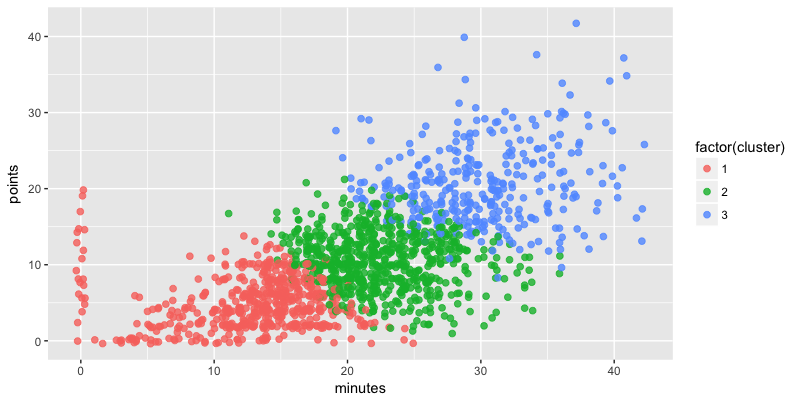
km_model <- support %>%
kmeans(centers = 3, nstart=20)
support$cluster <- km_model$cluster
ggplot(support, aes(minutes, points, col = factor(cluster))) +
geom_point(size = 2, alpha = 0.8, position = "jitter")
Mieux, n'est-ce pas ?
Et maintenant ?
Maintenant, nous voici avec un modèle de classement, et chaque nouvelle information entrante pourra être assignée à la classe qui lui correspond. Seulement voilà, nous vous entendons d'ici "oui, mais c'est bien, mais qu'est-ce qu'on en fait de ces classes ?" Vous avez raison, seules, ces classes ne servent qu'à indiquer qu'un point nouveau aura... le même comportement que les points anciens de sa même classe. Il convient à terme de qualifier les clusters, pour pouvoir les utiliser.
Ainsi, si nous devons prendre un exemple concret, les nouveaux visiteurs d'un site de ecommerce pourront être classés dans un cluster en fonction de leur parcours sur le site, en se basant sur les comportements des visiteurs précédents : visiteurs en balade, clients potentiels, clients qui n'ira pas au bout de son panier, et ainsi de suite. Le petit truc en plus ? Pouvoir adapter son algorithme au fur et à mesure de nouvelles entrées dans la base de données. Et là, ça sera le top !





Laisser un commentaire